Funzione gamma sui numeri reali In matematica, la funzione Gamma , nota anche come funzione gamma di Eulero è una funzione meromorfa, continua sui numeri reali positivi, che estende il concetto di fattoriale ai numeri complessi, nel senso che per ogni numero intero non negativo n {\displaystyle n}
Γ ( n + 1 ) = n ! {\displaystyle \Gamma (n+1)=n!} dove n ! {\displaystyle n!} n , {\displaystyle n,} 1 {\displaystyle 1} n {\displaystyle n} n ! = 1 ⋅ 2 ⋅ 3 ⋯ n {\displaystyle n!=1\cdot 2\cdot 3\cdots n}
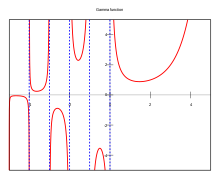
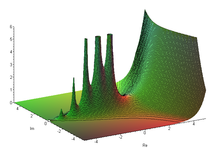
Definizione Valore assoluto della funzione gamma sul piano complesso La notazione Γ ( z ) {\displaystyle \Gamma (z)} z {\displaystyle z}
Γ ( z ) = ∫ 0 + ∞ t z − 1 e − t d t {\displaystyle \Gamma (z)=\int _{0}^{+\infty }t^{z-1}\,e^{-t}\,dt} converge assolutamente . Comunque, usando la continuazione analitica, si può estendere la definizione della Γ {\displaystyle \Gamma } z {\displaystyle z}
Γ ( z + 1 ) = z Γ ( z ) , {\displaystyle \Gamma (z+1)=z\Gamma (z)\,,} per cui si ha:
Γ ( z ) = Γ ( z + 1 ) z {\displaystyle \Gamma (z)={\frac {\Gamma (z+1)}{z}}} In questo modo, la definizione della Γ {\displaystyle \Gamma } R e ( z ) > 0 {\displaystyle \mathrm {Re} (z)>0} R e ( z ) > − 1 {\displaystyle \mathrm {Re} (z)>-1} z = 0 {\displaystyle z=0} z = 0 , − 1 , − 2 , … {\displaystyle z=0,-1,-2,\dots }
Siccome Γ ( 1 ) = 1 {\displaystyle \Gamma (1)=1} n {\displaystyle n}
Γ ( n + 1 ) = n ! . {\displaystyle \Gamma (n+1)=n!\,.} In statistica si incontra di frequente (per esempio nella variabile casuale normale) l'integrale:
∫ − ∞ + ∞ e − x 2 2 d x = 2 π {\displaystyle \int _{-\infty }^{+\infty }e^{-{\frac {x^{2}}{2}}}dx={\sqrt {2\pi }}} che si ottiene ponendo x 2 2 = t {\textstyle {\frac {x^{2}}{2}}=t} x = 2 t {\displaystyle x={\sqrt {2t}}} d x = 2 2 t d t {\textstyle dx={\frac {\sqrt {2}}{2{\sqrt {t}}}}dt}
∫ − ∞ + ∞ e − x 2 2 d x = 2 ∫ 0 + ∞ e − x 2 2 d x = 2 ∫ 0 + ∞ 2 2 t − 1 2 e − t d t = 2 Γ ( 1 2 ) = 2 π {\displaystyle {\begin{aligned}\int _{-\infty }^{+\infty }e^{-{\frac {x^{2}}{2}}}dx&=2\int _{0}^{+\infty }e^{-{\frac {x^{2}}{2}}}dx\\&=2\int _{0}^{+\infty }{\frac {\sqrt {2}}{2}}t^{-{\frac {1}{2}}}e^{-t}dt\\&={\sqrt {2}}\Gamma \left({\frac {1}{2}}\right)\\&={\sqrt {2\pi }}\end{aligned}}} Espressioni alternative Le seguenti espressioni alternative per la funzione Gamma, sono valide su tutto il piano complesso (ad eccezione dei poli):
Γ ( z ) = lim n → ∞ n ! n z z ( z + 1 ) ⋯ ( z + n ) {\displaystyle \Gamma (z)=\lim _{n\to \infty }{\frac {n!n^{z}}{z(z+1)\cdots (z+n)}}} dovuta a Gauss,
Γ ( z ) = e − γ z z ∏ n = 1 ∞ ( 1 + z n ) − 1 e z / n {\displaystyle \Gamma (z)={\frac {e^{-\gamma z}}{z}}\prod _{n=1}^{\infty }\left(1+{\frac {z}{n}}\right)^{-1}e^{z/n}} dove γ {\displaystyle \gamma } Schlömilch e ottenibile applicando il teorema di fattorizzazione di Weierstrass alla funzione 1 Γ ( z ) {\displaystyle {\frac {1}{\Gamma (z)}}}
1 Γ ( z ) = z e γ z ∏ n = 1 ∞ ( 1 + z n ) e − z n {\displaystyle {\frac {1}{\Gamma (z)}}=ze^{\gamma z}\prod _{n=1}^{\infty }\left(1+{\frac {z}{n}}\right)e^{-{\frac {z}{n}}}} Un'ulteriore espressione alternativa è la seguente:
Γ ( z ) = ∑ n = 0 + ∞ ( − 1 ) n n ! 1 z + n + ∫ 1 + ∞ t z − 1 e − t d t . {\displaystyle \Gamma (z)=\sum _{n=0}^{+\infty }{\frac {(-1)^{n}}{n!}}{\frac {1}{z+n}}+\int _{1}^{+\infty }t^{z-1}e^{-t}dt.} In questa formula sono espliciti i poli di ordine 1 {\displaystyle 1} ( − 1 ) n n ! {\displaystyle {\frac {(-1)^{n}}{n!}}} z = − n {\displaystyle z=-n} n {\displaystyle n}
La singolarità nell'origine può essere anche dedotta dalla relazione di ricorrenza . Infatti
lim z → 0 Γ ( z ) = lim z → 0 Γ ( z + 1 ) z = lim z → 0 1 z , {\displaystyle \lim _{z\to 0}\Gamma (z)=\lim _{z\to 0}{\frac {\Gamma (z+1)}{z}}=\lim _{z\to 0}{\frac {1}{z}},} dove è stato fatto uso della relazione Γ ( 1 ) = 1 {\displaystyle \Gamma (1)=1}
Proprietà Altre importanti proprietà della funzione Gamma sono la formula di riflessione di Eulero:
Γ ( 1 − z ) Γ ( z ) = π sin ( π z ) , z ∉ Z , {\displaystyle \Gamma (1-z)\Gamma (z)={\pi \over \sin(\pi z)},\qquad z\not \in \mathbb {Z} ,} e quella di duplicazione:
Γ ( z ) Γ ( z + 1 2 ) = 2 1 − 2 z π Γ ( 2 z ) {\displaystyle \Gamma (z)\Gamma \left(z+{\frac {1}{2}}\right)=2^{1-2z}{\sqrt {\pi }}\,\Gamma (2z)} che a sua volta è un caso particolare della formula di moltiplicazione:
Γ ( z ) Γ ( z + 1 m ) Γ ( z + 2 m ) ⋯ Γ ( z + m − 1 m ) = ( 2 π ) ( m − 1 ) / 2 m 1 / 2 − m z Γ ( m z ) {\displaystyle \Gamma (z)\Gamma \left(z+{\frac {1}{m}}\right)\Gamma \left(z+{\frac {2}{m}}\right)\cdots \Gamma \left(z+{\frac {m-1}{m}}\right)=(2\pi )^{(m-1)/2}m^{1/2-mz}\Gamma (mz)} la quale per z = 0 {\displaystyle z=0}
Γ ( 1 m ) Γ ( 2 m ) ⋯ Γ ( m − 1 m ) = ( 2 π ) ( m − 1 ) / 2 m {\displaystyle \Gamma \left({\frac {1}{m}}\right)\Gamma \left({\frac {2}{m}}\right)\cdots \Gamma \left({\frac {m-1}{m}}\right)={\frac {(2\pi )^{(m-1)/2}}{\sqrt {m}}}} Quest'ultima identità è ottenibile anche dalla formula di riflessione e dall'identità trigonometrica ∏ k = 1 m − 1 sin k π m = m 2 m − 1 {\displaystyle \prod _{k=1}^{m-1}\sin {\frac {k\pi }{m}}={\frac {m}{2^{m-1}}}}
Le derivate della funzione Gamma:
Γ ( n ) ( z ) = ∫ 0 + ∞ [ ln ( t ) ] n t z − 1 e − t d t {\displaystyle \Gamma ^{(n)}(z)=\int _{0}^{+\infty }[\ln {(t)}]^{n}\,t^{z-1}\,e^{-t}\,dt} possono essere espresse in funzione della stessa funzione Gamma e di altre funzioni, per esempio:
Γ ′ ( z ) = Γ ( z ) ψ 0 ( z ) , {\displaystyle \Gamma '(z)=\Gamma (z)\psi _{0}(z),} dove ψ 0 {\displaystyle \psi _{0}} funzione poligamma di ordine zero. In particolare,
Γ ′ ( 1 ) = − γ , {\displaystyle \Gamma '(1)=-\gamma ,} dove γ {\displaystyle \gamma } costante di Eulero-Mascheroni .
Si ha, inoltre:
d d z ln Γ ( z ) = Γ ′ ( z ) Γ ( z ) = ψ 0 ( z ) = − γ − 1 z − ∑ n = 1 ∞ ( 1 n + z − 1 n ) {\displaystyle {\frac {d}{dz}}\ln {\Gamma {(z)}}={\frac {\Gamma '{(z)}}{\Gamma {(z)}}}=\psi _{0}(z)=-\gamma -{\frac {1}{z}}-\sum _{n=1}^{\infty }\left({\frac {1}{n+z}}-{\frac {1}{n}}\right)} che per z = m {\displaystyle z=m}
ψ 0 ( m ) = Γ ′ ( m ) Γ ( m ) = − γ + 1 + 1 2 + ⋯ + 1 m − 1 = − γ + H m − 1 {\displaystyle \psi _{0}(m)={\frac {\Gamma '{(m)}}{\Gamma {(m)}}}=-\gamma +1+{\frac {1}{2}}+\dots +{\frac {1}{m-1}}=-\gamma +H_{m-1}} dove H m − 1 {\displaystyle H_{m-1}} numero armonico .
Derivando membro a membro rispetto a z {\displaystyle z}
d d z Γ ′ ( z ) Γ ( z ) = ψ 1 ( z ) = ∑ n = 0 ∞ 1 ( n + z ) 2 {\displaystyle {\frac {d}{dz}}{\frac {\Gamma '{(z)}}{\Gamma {(z)}}}=\psi _{1}(z)=\sum _{n=0}^{\infty }{\frac {1}{(n+z)^{2}}}} che per z = 0 {\displaystyle z=0} z = 1 {\displaystyle z=1} serie armonica generalizzata di ordine 2
[ d d z Γ ′ ( z ) Γ ( z ) ] z = 1 = ψ 1 ( 1 ) = ∑ n = 0 ∞ 1 ( n + 1 ) 2 = ∑ n = 1 ∞ 1 n 2 = ζ ( 2 ) = π 2 6 {\displaystyle \left[{\frac {d}{dz}}{\frac {\Gamma '{(z)}}{\Gamma {(z)}}}\right]_{z=1}=\psi _{1}(1)=\sum _{n=0}^{\infty }{\frac {1}{(n+1)^{2}}}=\sum _{n=1}^{\infty }{\frac {1}{n^{2}}}=\zeta (2)={\frac {\pi ^{2}}{6}}} Lukacs studiò altre proprietà nell'opera A Characterization of the Gamma Distribution negli Annals of Mathematical Statistics del 1955 .
Ricordiamo anche che, a partire dalla funzione Gamma, la funzione poligamma di ordine m {\displaystyle m}
ψ m ( z ) := ( d d z ) m + 1 ln Γ ( z ) = ( d d z ) m Γ ′ ( z ) Γ ( z ) = ( d d z ) m ψ 0 ( z ) {\displaystyle \psi _{m}(z):=\left({\frac {d}{dz}}\right)^{m+1}\ln {\Gamma (z)}=\left({\frac {d}{dz}}\right)^{m}{\frac {\Gamma '(z)}{\Gamma (z)}}=\left({\frac {d}{dz}}\right)^{m}\psi _{0}(z)} Valori notevoli Probabilmente, il più noto valore che la funzione Gamma assume su numeri non interi è:
Γ ( 1 2 ) = π , {\displaystyle \Gamma \left({\frac {1}{2}}\right)={\sqrt {\pi }},} che si può trovare ponendo z = 1 2 {\displaystyle z={\frac {1}{2}}}
Oltre a questo e al già citato valore assunto sui numeri naturali , sono interessanti anche le seguenti proprietà, che interessano i multipli dispari di 1 2 {\displaystyle {\frac {1}{2}}}
Γ ( n 2 ) = ( n − 2 ) ! ! 2 ( n − 1 ) / 2 π = ( n 2 − 1 n − 1 2 ) ( n − 1 2 ) ! π {\displaystyle \Gamma \left({\frac {n}{2}}\right)={\frac {(n-2)!!}{2^{(n-1)/2}}}{\sqrt {\pi }}={{\frac {n}{2}}-1 \choose {\frac {n-1}{2}}}\left({\frac {n-1}{2}}\right)!{\sqrt {\pi }}} Γ ( − n 2 ) = π ( − 1 / 2 n + 1 2 ) ( n + 1 2 ) ! {\displaystyle \Gamma \left(-{\frac {n}{2}}\right)={\frac {\sqrt {\pi }}{{\Biggl (}{\begin{matrix}-1/2\\{\frac {n+1}{2}}\end{matrix}}{\Biggr )}\left({\frac {n+1}{2}}\right)!}}} dove n ! ! {\displaystyle n!!} semifattoriale e la parentesi tonda a due livelli il coefficiente binomiale .
Teorema di unicità Il teorema di Bohr-Mollerup afferma che, tra tutte le funzioni che estendono la funzione fattoriale, solo la funzione Gamma è tale che il suo logaritmo è una funzione convessa .
Bibliografia Donato Greco, Complementi di Analisi , capitolo 12, Napoli, Liguori Editore, 1978, pp. 227-248, ISBN 88-207-0325-4. Nicola Fusco, Paolo Marcellini , Carlo Sbordone , Analisi Matematica Due , capitolo 8, Napoli, Liguori Editore, 1996, ISBN 978-88-207-2675-1. (EN Handbook of Mathematical Functions (DE Handbuch der theorie der gammafunktion , Lipsia, 1906. Voci correlate Altri progetti Wikimedia Commons contiene immagini o altri file su funzione Gamma Collegamenti esterni Controllo di autorità GND (DE · NDL (EN , JA
Portale Matematica : accedi alle voci di Wikipedia che trattano di matematica
 Wikimedia Commons contiene immagini o altri file su funzione Gamma
Wikimedia Commons contiene immagini o altri file su funzione Gamma

 Portale Matematica: accedi alle voci di Wikipedia che trattano di matematica
Portale Matematica: accedi alle voci di Wikipedia che trattano di matematica




































![{\displaystyle \Gamma ^{(n)}(z)=\int _{0}^{+\infty }[\ln {(t)}]^{n}\,t^{z-1}\,e^{-t}\,dt}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f642585e2f3ff3e135f18f3ae870b0d6992ccaee)









![{\displaystyle \left[{\frac {d}{dz}}{\frac {\Gamma '{(z)}}{\Gamma {(z)}}}\right]_{z=1}=\psi _{1}(1)=\sum _{n=0}^{\infty }{\frac {1}{(n+1)^{2}}}=\sum _{n=1}^{\infty }{\frac {1}{n^{2}}}=\zeta (2)={\frac {\pi ^{2}}{6}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a426d25fac1a62bca27f601d134d24696c3ea039)





















