収束級数

数学において、収束級数（しゅうそくきゅうすう、英: convergent series）とは、その部分和の成す数列が収束するような級数である。

ここで、級数とは数列の項の総和のことであり、与えられた数列 a₁, a₂, ..., a_n, ... の第 n-部分和とは最初の n-項の有限和

S_{n}=\sum _{k=1}^{n}a_{k}

のことを指す。

ある級数が収束級数であることは、「（有限な）和を持つ」とか「和が有限確定である」などと言い表される。

定義

厳密に言えば、級数が「通常の意味で」収束するとは、定数 l が存在して、任意の正の数 ε > 0 に対して十分大きな整数 N = N_ε をうまくとれば、n ≥ N なる任意の整数 n に対して

|S_{n}-l|\leq \varepsilon

を満たすことをいう。収束しない級数は発散するという。

級数の収束・発散の例

すべての自然数の逆数和は発散する。（調和級数）

${1 \over 1}+{1 \over 2}+{1 \over 3}+{1 \over 4}+{1 \over 5}+{1 \over 6}+\cdots =\sum _{n=1}^{\infty }{\frac {1}{n}}\to \infty$

すべての自然数の逆数の交代和（各項の符号が交代的に入れ替わる級数）はln2に収束する。（2の自然対数）

${1 \over 1}-{1 \over 2}+{1 \over 3}-{1 \over 4}+{1 \over 5}-{1 \over 6}+\cdots =\sum _{n=1}^{\infty }(-1)^{n-1}{\frac {1}{n}}=\ln 2$

すべての正の奇数の逆数の交代和は収束し、 $\pi /4$ に等しい。（ライプニッツの公式）

${1 \over 1}-{1 \over 3}+{1 \over 5}-{1 \over 7}+{1 \over 9}-{1 \over 11}+\cdots =\sum _{n=1}^{\infty }(-1)^{n-1}{\frac {1}{2n-1}}={\pi \over 4}$

すべての素数の逆数和は発散する。（n番目の素数を $p_{n}$ とする）

${1 \over 2}+{1 \over 3}+{1 \over 5}+{1 \over 7}+{1 \over 11}+{1 \over 13}+\cdots =\sum _{n=1}^{\infty }{\frac {1}{p_{n}}}\to \infty$

すべての三角数の逆数和は2に収束する。

${1 \over 1}+{1 \over 3}+{1 \over 6}+{1 \over 10}+{1 \over 15}+{1 \over 21}+\cdots =\sum _{n=1}^{\infty }{\frac {1}{\frac {n(n+1)}{2}}}=2$

すべての階乗数の逆数和は収束してネイピア数と等しい。

${\frac {1}{1}}+{\frac {1}{1}}+{\frac {1}{2}}+{\frac {1}{6}}+{\frac {1}{24}}+{\frac {1}{120}}+\cdots =\sum _{n=0}^{\infty }{\frac {1}{n!}}=e$

すべての平方数の逆数和が収束することはバーゼル問題といい、オイラーが肯定的に解決した。これはリーマンゼータ関数の 2 における値 ζ(2) である。

${1 \over 1}+{1 \over 4}+{1 \over 9}+{1 \over 16}+{1 \over 25}+{1 \over 36}+\cdots =\sum _{n=1}^{\infty }{\frac {1}{n^{2}}}={\pi ^{2} \over 6}$

すべての2の冪の逆数和は2に収束する。

${1 \over 1}+{1 \over 2}+{1 \over 4}+{1 \over 8}+{1 \over 16}+{1 \over 32}+\cdots =\sum _{n=1}^{\infty }\left({\frac {1}{2}}\right)^{n-1}=2$

すべての立方数の逆数和は収束し、この値 ζ(3) （アペリーの定数）は無理数であることが証明されている。（アペリーの定理）

${1 \over 1}+{1 \over 8}+{1 \over 27}+{1 \over 64}+{1 \over 125}+{1 \over 216}+\cdots =\sum _{n=1}^{\infty }{\frac {1}{n^{3}}}=1.2020569...$

すべてのフィボナッチ数の逆数和は収束し、この値は無理数であることが証明されている。（フィボナッチ数列の逆数和）

${1 \over 1}+{1 \over 1}+{1 \over 2}+{1 \over 3}+{1 \over 5}+{1 \over 8}+\cdots =\sum _{n=1}^{\infty }{\frac {1}{F_{n}}}=3.359885666...$

収束判定法

詳細は「収束判定法（英語版）」を参照

与えられた級数が収束または発散することの判定法はさまざまなものが知られる。

比較判定法 (comparison test)

数列 (a_n) の各項が、別の数列 (b_n) の各項と比較して、任意の n に対し 0 ≤ a_n ≤ b_n が成り立つものとする。このとき

∑ b_n が収束するならば ∑ a_n は収束する。
∑ a_n が発散するならば ∑ b_n は発散する。

の二つの命題が成り立つ。

ダランベールの収束判定法（比判定法、ratio test）

複素数列 (a_n) に対し、

\lim _{n\to \infty }\left|{\frac {a_{n+1}}{a_{n}}}\right|=r

なる定数 r が存在するものと仮定する。

r < 1 ならば級数 Σa_n は収束し、r > 1 ならば級数は発散する。r = 1 のときはこの判定法では収束するとも発散するともいえない。

コーシーの冪根判定法 (root test)

対象となる級数の各項は複素数であるものとし、

r=\limsup _{n\to \infty }{\sqrt[{n}]{|a_{n}|}}

とする。

r < 1 ならば級数 Σa_n は収束し、r > 1 ならば級数は発散するが、r = 1 のときはこの判定法では収束するとも発散するとも判定することはできない。

比の判定法も冪根の判定法も、幾何級数の挙動と比べることに基づく判定法であり、これらの判定法が有効な場面というのも似通っている。実は、比の判定法が有効な（極限が存在して 1 ではない）とき、冪根判定法は常に有効だが、逆は正しくない。つまり冪根判定法のほうが適用範囲は広いのだが、実用上の問題として、よくある種類の級数に対してこのような冪根の極限を計算することは難しいことが多いという点がある。

積分判定法

与えられた級数をなんらかの積分と比較することで収束・発散を判定する方法がある。数列 (a_n) に対して f(n) = a_n となる正値単調減少関数が存在するならば、

\int _{1}^{\infty }f(x)\,dx=\lim _{t\to \infty }\int _{1}^{t}f(x)\,dx<\infty ,

のとき級数は収束し、積分が発散するならば級数は同様に発散する。

極限比較法（英語版）

正の項からなる数列 (a_n), (b_n) について、各項の比 a_n/b_n が 0 でない有限な極限をもつならば

\sum _{n=1}^{\infty }a_{n}<\infty \iff \sum _{n=1}^{\infty }b_{n}<\infty

が成り立つ。

ライプニッツの判定法

交代級数の収束判定法は、

\sum _{n=1}^{\infty }(-1)^{n}a_{n}

の形の交代級数が、正値数列 (a_n) が単調減少で 0 に収束するならばもとの級数も収束する（十分条件）というものである。

コーシーの凝集判定法

(a_n) が単調減少列ならば

\sum _{n=1}^{\infty }a_{n}<\infty \iff \sum _{k=1}^{\infty }2^{k}a_{2^{k}}<\infty

が成立する。

ディリクレの判定法

アーベルの判定法（英語版）

ラーベの判定法（英語版）

条件収束と絶対収束

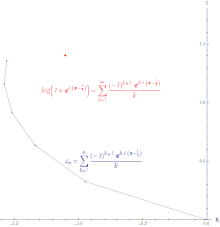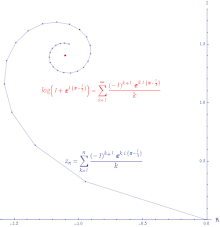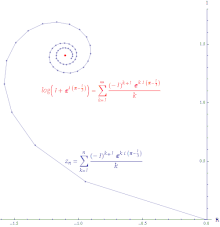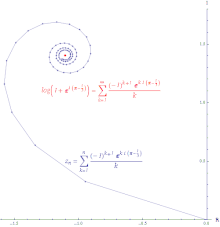対数関数 log(1 + z) の 0 の周りでのテイラー級数の、z = exp(π − i/3) での値の条件収束の様子を示したもの。この線の長さは無限大である。

任意の数列 (a₁, a₂, ...) に対して、a_n ≤ |a_n| が任意の n について成立するから、

\left|\sum _{n=1}^{\infty }a_{n}\right|\leq \sum _{n=1}^{\infty }|a_{n}|

がわかる。これはつまり、右辺が収束するならば、もとの級数も収束することを示している（逆は成り立たない）。

無限級数 ∑|a_n| が収束するならば、無限級数 ∑ a_n は絶対収束 (absolutely convergent) するという。絶対収束級数の部分和の成す増大列から各値を結んで得られる折れ線は有限の長さを持つ。指数関数のテイラー級数は至る所絶対収束する。

無限級数 ∑ a_n が収束して、無限級数 ∑|a_n| は発散するならば、無限級数 ∑ a_n は条件収束 (conditionally convergent) するという。条件収束級数の部分和の値をつないで得られる線分は長さが無限大となる。対数関数のテイラー級数は収束域の各点で条件収束する。

リーマンの級数定理（英語版）は「条件収束級数はその項を並べ替えることにより任意の値に収束させ、あるいは発散させることができる」ということを述べるものである。

条件収束という代わりに半収束 (semiconvergent) ということもある。逆に絶対収束の代わりに無条件収束 (unconditionally convergent) ともいう。

一様収束

詳細は「一様収束」を参照

(f₁, f₂, ...) を関数列とする。関数項級数

\sum _{n=1}^{\infty }f_{n}

が、関数 f に一様収束する (converge uniformly) とは

s_{n}(x)=\sum _{k=1}^{n}f_{k}(x)

で定義される部分和関数列 (s_n) が f に一様収束することを言う。

比較判定法の関数項無限級数における対応物が存在して、ワイエルシュトラスのM判定法と呼ばれる。

コーシーの判定法

実数列に関するコーシーの判定法によれば、実数を項とする級数

\sum _{n=1}^{\infty }a_{n}

が収束する必要十分条件はその部分和の列がコーシー列を成すことである。すなわち、任意の正数 ε > 0 に対し正整数 N が存在して、n ≥ m ≥ N なる全ての m, n について

\left|\sum _{k=m}^{n}a_{k}\right|<\varepsilon

が成り立つということであり、またこれを

\lim _{n\to \infty \atop m\to \infty }\sum _{k=n}^{n+m}a_{k}=0

という形に述べることもできる。

参考文献

Walter, Rudin (1976), Principles of Mathematical Analysis, McGrawHill
Michael, Spivak (1994), Calculus (3rd ed.), Houston Texas: Publish or Perish, Inc., ISBN 0-914098-89-6

外部リンク

Chase, Robert (2007). More plots on convergence
Weisstein, Eric (2005). Riemann Series Theorem. Retrieved May 16, 2005.

級数・数列

等差数列

発散級数	1 + 1 + 1 + 1 + ⋯ 1 + 2 + 3 + 4 + ⋯ 無限算術級数

等比数列

収束級数	1/2 − 1/4 + 1/8 − 1/16 + ⋯ 1/2 + 1/4 + 1/8 + 1/16 + ⋯ 1/4 + 1/16 + 1/64 + 1/256 + ⋯
発散級数	1 + 1 + 1 + 1 + ⋯ 1 + 2 + 4 + 8 + ⋯ 1 − 2 + 4 − 8 + ⋯ グランディ級数

整数列

その他の数列

発散級数	1 − 2 + 3 − 4 + ⋯ 1 − 1 + 2 − 6 + 24 − 120 + ⋯ 調和級数
収束級数	交項級数幾何級数超幾何級数 q超幾何級数ライプニッツの公式