Polinom

Matematika
A matematika alapjai
Halmazelmélet · Naiv halmazelmélet Axiomatikus halmazelmélet · Matematikai logika
Algebra
Elemi algebra · Lineáris algebra · Polinomok Absztrakt algebra · Csoportelmélet · Gyűrűelmélet · Testelmélet Mátrixok · Univerzális algebra
Analízis
Valós analízis · Komplex analízis · Vektoranalízis Differenciálegyenletek · Funkcionálanalízis Mértékelmélet
Geometria
Euklideszi geometria · Nemeuklideszi geometria Affin geometria · Projektív geometria Differenciálgeometria · Algebrai geometria Topológia
Számelmélet
Algebrai számelmélet · Analitikus számelmélet
Diszkrét matematika
Kombinatorika · Gráfelmélet · Játékelmélet Algoritmusok · Formális nyelvek Információelmélet
Alkalmazott matematika
Numerikus analízis · Valószínűségszámítás Statisztika · Káoszelmélet · Matematikai fizika Matematikai biológia · Gazdasági matematika Kriptográfia
Általános
Matematikusok · Matematikatörténet Matematikafilozófia · Portál
Sablon:Matematika m v sz

A matematikában a polinom (avagy többtagú algebrai egész kifejezés) egy olyan kifejezés, melyben csak számok és változók nemnegatív egész kitevőjű hatványainak szorzatai, illetve ilyenek összegei szerepelnek. Például:

p(x,y,z,u) = 5x⁴y⁶ - 3xz³+11y¹⁵u⁷

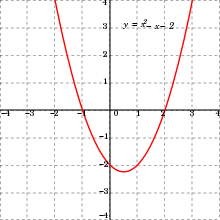
q(x) = 2x² + 6x + 9

r(x,y) = x³ + 3x²y + 3x²y + y³

A polinomban a számokkal szorzott hatványszorzatokat monomoknak (avagy egytagú algebrai egész kifejezésnek) nevezzük (például p-nél az 5x⁴y⁶, a -3xz³ és a 11y¹⁵u⁷ tagok).

Történet

A polinom gyökeinek meghatározása, vagyis különféle algebrai egyenletek megoldása már régóta a matematika fontos problémái közé tartozik. A mai praktikus jelölések a 15. században kezdtek el kifejlődni, addig általában az volt a szokás, hogy egy egyenletet szavakkal írtak le vagy az ókori Kínában például a változók szerint „ábrákat” készítettek róluk.

Az egyenlőségjelet először Robert Recorde használta a 16. században, és ugyanebben az időben terjedt el a „+” jel használata az összeadásra, valamint a „−” jel használata a kivonásra. René Descartes volt az, aki elkezdte terjeszteni azt a ma is használt jelölésmódot, hogy a konstansok leírására az ábécé elejéről választunk betűket, míg a változókhoz az ábécé végéről. És ugyancsak ő volt az, aki először felső indexbe írta egy változó kitevőjét.

Az elemi algebrában

Az elemi algebrában P(x) egyváltozós polinom, ha:

${\displaystyle P(x)=\sum _{i=0}^{n}a_{i}x^{i}=a_{0}+a_{1}x+a_{2}x^{2}+\dotsb +a_{n-1}x^{n-1}+a_{n}x^{n},\quad n\geq 0}$.

Itt x a polinom változója, n a polinom foka. Vannak többváltozós polinomok is, ezekben több változó szerepel. Egy többváltozós polinom foka az a legnagyobb szám, amit az egyes tagok tényezőinek kitevőinek összeadásával kapunk. Minden kitevőnek nemnegatív egész számnak kell lennie.

A polinom tagjaiban a számot együtthatónak, az ismeretlenekből álló szorzatot monomnak vagy egytagnak nevezik. A nulladfokú tag együtthatója konstans tag. Az elsőfokúé lineáris, a másodfokúé kvadratikus, a harmadfokúé kubikus tag. Általában ha egy változó az első hatványon szerepel, akkor nem szokták a kitevőbe kiírni az 1-et. A 0 fokú monomokat konstans polinomoknak nevezzük.

Például az

${\displaystyle 8x^{3}-7x^{2}+36\,\!}$

egy egyváltozós, harmadfokú polinom. Az x fokszáma szerint csökkenő sorrendbe írva, az első monom foka 3, a másodiké 2, a harmadiké 0. A harmadfokú tag együtthatója 8, a másodfokúé -7, a konstans tag 36.

A valós együtthatós polinomfüggvények értelmezhetők a teljes valós számegyenesen, a komplex együtthatós polinomok pedig értelmezhetők a teljes komplex számsíkon.

Nullpolinom az a polinom, aminek összes együtthatója nulla. Ennek foka mínusz végtelen. Ha a főegyüttható egy, akkor a polinom normált.

A polinom szimmetrikus, ha bárhogy cseréljük fel (permutáljuk) benne az ismeretleneket, változatlan marad.

Egy másik jellegzetes polinomfajta a homogén fokszámú polinomok, melyekben a monomok foka egyenlő. Ilyenek szerepelnek például a binomiális tételben:

${\displaystyle (a+b)^{4}=a^{4}+4a^{3}b+6a^{2}b^{2}+4ab^{3}+b^{4}\,}$

Egyneműnek nevezünk két (vagy több) monomot, ha csak együtthatóikban különböznek. Polinomokat úgy adunk össze, hogy az egynemű egytagúak együtthatóit összeadjuk:

${\displaystyle {\begin{matrix}p(x,y)&=&5x^{2}y&+2xy^{2}&+6y^{3}\\q(x,y,z)&=&2x^{2}y&-7xy^{2}&+8yz^{6}\\&&&&\\(p+q)(x,y,z)&=&7x^{2}y&-5xy^{2}&+6y^{3}&+8yz^{6}\end{matrix}}}$

Az n ismeretlenes polinomoknak az egyneműek összevonása után legfeljebb

${\displaystyle {\binom {n+k-1}{k}},}$

k fokú monomja lehet.

Az egynemű monomok összevonása után az n-edfokú polinomnak legfeljebb

${\displaystyle {\binom {n+k}{k}}}$

monomja lehet.

A szorzás úgy történik, hogy „minden tagot minden taggal beszorzunk” és a keletkező szorzatokban az azonos változók hatványait az azonos alapú hatványok szorzásának szabályával számítjuk ki. Például

${\displaystyle p(x,y)=x^{2}+xy\,}$

${\displaystyle q(x,z)=3x^{3}-7z^{2}\,}$

${\displaystyle (p\cdot q)(x,y,z)=x^{2}\cdot 3x^{3}+x^{2}\cdot (-7z^{2})+xy\cdot 3x^{3}+xy\cdot (-7z^{2})=\,}$

${\displaystyle =3x^{5}+(-7)x^{2}z^{2}+3x^{4}y+(-7)xyz^{2}\,}$

Emellett a számmal való szorzás művelete is értelmes: minden együtthatót beszorzunk az adott számmal. Például

${\displaystyle p(x,y)=5x^{2}y+2xy^{2}+6y^{3},}$

${\displaystyle 3\cdot p(x,y)=3\cdot 5x^{2}y+3\cdot 2xy^{2}+3\cdot 6y^{3}=15x^{2}y+6xy^{2}+18y^{3},}$

Ha ${\displaystyle f,g}$ polinomok, akkor szorzatuk fokszáma becsülhető:

${\displaystyle \deg(f+g)\leq \max(\deg f,\deg g)}$

Valós, illetve komplex polinomok esetén:

${\displaystyle \deg(f\cdot g)=\deg f+\deg g.}$

A polinomok halmaza zárt a helyettesítésre, azaz ha egy ismeretlenbe mindenhová polinomot helyettesítünk, akkor újra polinomot kapunk. Ez csak akkor igaz, ha a változók számát nem korlátozzuk, mert egy helyettesítés új változókat hozhat be. De ha csak a már meglevő változókat használja, akkor a változók száma megmarad.

Gyűrű fölötti polinomok

Polinomok tetszőleges gyűrű fölött definiálhatók, ekkor a polinom együtthatói a gyűrű elemei közül kerülnek ki. Ha R ez a gyűrű, akkor az egyváltozós, R-beli együtthatós polinomok körét R[X] jelöli. R[X] maga is gyűrűt alkot. Ha T test (algebra), akkor T[X] végtelen dimenziós vektorteret T felett. Ha T kommutatív test és a T[X] integritási tartományban p felbonthatatlan elem, akkor az T[X]/(p) maradékosztálygyűrű test. A középiskolában egész, racionális vagy valós együtthatós polinomokkal találkozhatunk. Az algebra alaptételében komplex együtthatós polinomokról van szó. Hasznosak még a kvaternió együtthatós (tehát lényegében mátrix együtthatójú), vagy a modulo m maradékosztálybeli együtthatós (véges testbeli) polinomok is. Ha polinomgyűrű fölött veszünk polinomgyűrűt, akkor többváltozós polinomgyűrűhöz jutunk.

A változókat néha határozatlanoknak nevezik. Az egyes monomokban a változók kitevőinek összege adja meg az adott monom fokát. A polinom fokának a benne lévő monomok fokának maximumát tekintjük.

Gyűrű fölötti polinomok esetén az összeg fokának becslésére csak akkor használható a fenti képlet, ha a gyűrű integritási tartomány. Tehát integritási tartomány fölött

${\displaystyle \deg(f\cdot g)=\deg f+\deg g,}$

általános esetben ${\displaystyle {\mathord {\leq }}}$ a becslés. A szorzat fokának becslése ugyanaz, mint valós fölött.

A lineáris algebrában adott n-re a legfeljebb n-edfokú adott test fölötti polinomok vektorteret alkotnak, aminek dimenziója n + 1.

A mátrixok karakterisztikus polinomját többek között a mátrixok diagonalizálásához használják.

Ha R gyűrű, akkor R[X] is gyűrű, amit polinomgyűrűnek neveznek. Ez megkapható úgy, mint R bővítése algebrailag független elemmel. A polinomokat egyértelműen lehet jellemezni együtthatóik véges sorozatával, ahol az összeadás tagonkénti összeadás, a szorzat konvolúció, és a konstanssal (gyűrűelemmel) való szorzás is tagonként kell végezni.

${\displaystyle a+b:=(a_{n}+b_{n})_{n\in \mathbb {N} _{0}}}$

és

${\displaystyle a\cdot b:=\left(\sum _{i=0}^{n}a_{i}b_{n-i}\right)_{n\in \mathbb {N} _{0}}=\left(\sum _{i+j=n}a_{i}b_{j}\right)_{n\in \mathbb {N} _{0}},}$

Ezzel a polinomgyűrű algebrát alkot. Habár ez a konstrukció nem használja a határozatlant, a behelyettesítés is értelmezhető műveletként. Ezzel behelyettesítési homomorfizmushoz jutunk. Ha az alapgyűrű kommutatív, egységelemes, nullosztómentes, akkor a polinomgyűrű is kommutatív, egységelemes, nullosztómentes lesz.^[1]

Különböző polinomok definiálhatják ugyanazt a polinomfüggvény, különösen ha vannak nullosztók, vagy ha a test véges. Például legyen ${\displaystyle R}$ a ${\displaystyle \mathbb {Z} /3\mathbb {Z} =\{{\bar {0}},{\bar {1}},{\bar {2}}\}}$ maradékosztálygyűrű, így az ${\displaystyle f,g\in (\mathbb {Z} /3\mathbb {Z} )[X]}$

${\displaystyle f=X(X-{\bar {1}})(X-{\bar {2}})=X^{3}-{\bar {3}}X^{2}+{\bar {2}}X=X^{3}-X}$ és a ${\displaystyle g=0}$ polinomok ugyanazt a függvényt állítják elő. Végtelen integritástartomány esetén ez nem fordulhat elő.

Számelméletük

Bővebben: Polinomok számelmélete

Polinomfüggvények

Bővebben: Polinomfüggvény

Ha R[X] az R gyűrű feletti polinomgyűrű és p = p(x) polinom, akkor a p által meghatározott polinomfüggvényen a

${\displaystyle p:R\longrightarrow R;\quad x\mapsto p(x)}$

függvényt értjük.

Példák:

1. a komplex számok feletti q(z) = iz⁴ + 3iz - 5 polinom által meghatározott polinomfüggvény a

g: C ${\displaystyle \rightarrow }$ C; z ${\displaystyle \mapsto }$ iz⁴ + 3iz - 5

függvény

2. a modulo 5 maradékosztályok feletti r(x) = x⁴ polinom által meghatározott polinomfüggvény a

h: Z₅ ${\displaystyle \rightarrow }$ Z₅; x ${\displaystyle \mapsto }$ x⁴

Véges gyűrű feletti polinomfüggvény nem jelöli ki egyértelműen azt a polinomot, melyből a polinomfüggvény keletkezett. A 2. példánál h nem más, mint a

${\displaystyle h_{1}(x)=\left\{{\begin{matrix}0&{\mbox{ ha }}x=0\\1&{\mbox{ ha }}x=1,2,3,4\end{matrix}}\right.}$

függvény éspedig a kis Fermat-tétel miatt. De ez ugyanaz, mint a h₂(x)= x⁸ polinomfüggvény, amely azonban más polinom által meghatározott. S míg x⁴ ${\displaystyle \neq }$ x⁸ (mint polinom), addig h₁ = h₂, mint függvény. Ez amiatt van, hogy míg polinomból végtelen sok van, addig R-ből R-be menő függvényből csak nⁿ db, amennyiben R számossága az n véges szám.

Helyettesítési érték, zérushely, gyök

Ha p ∈ R[X] polinom és α ∈ R, akkor azt mondjuk, hogy p helyettesítési értéke α-ban a β ∈ R elem, ha a p által meghatározott polinomfüggvény α-n a β-t veszi föl értékül. Ezt a következőképpen jelöljük:

${\displaystyle p(\alpha )=\beta \,}$

Ha p osztható az (x - α) elsőfokú polinommal, azaz létezik olyan q ∈ R[X] polinom, hogy

${\displaystyle p(x)=(x-\alpha )\cdot q(x)}$

akkor azt mondjuk, hogy α ∈ R elem gyöke a p polinomnak és hogy (x-α) gyöktényezője p-nek.

Az x₀ ∈ R elem zérushelye a p polinomnak, ha x₀-ben a p helyettesítési értéke 0.

Bézout tétele – A p ∈ R[X] polinomnak az α ∈ R elem pontosan akkor gyöke, ha zérushelye.

Test fölött nemnulla polinom gyökeinek száma legfeljebb annyi, mint a fokszáma. A komplex számok körében, vagy más algebrailag zárt test fölött ezen kívül még az is igaz, hogy egy nemkonstans polinomnak pontosan annyi gyöke van (a multiplicitással számolva) ahányadfokú a polinom. Ez az algebra alaptétele.

A (multiplicitással számolva) pontosan n gyökű n-edfokú polinomok felírhatók ún. gyöktényezős alakban:

${\displaystyle f(x)=a_{n}x^{n}+a_{n-1}x^{n-1}+\dots +a_{1}x+a_{0}=a_{n}(x-x_{1})(x-x_{2})\dots (x-x_{n})}$

A jobb oldali alakban ${\displaystyle a_{n}}$ a polinom főegyütthatójának, ${\displaystyle x_{1},x_{2},\dots ,x_{n}}$ pedig a polinom gyökeinek felelnek meg. Végtelen gyűrű fölött teljesül a kölcsönös meghatározottság.

Gyökök meghatározása, becslése

Egész együtthatós polinom racionális gyökeinek meghatározásában segít a Rolle-féle gyöktétel. A jelöltek az x=p/q alakú racionális számok, ahol p és q relatív prímek, és p osztója a konstans tagnak, és q osztója a főegyütthatónak. Alacsony fokú, legfeljebb negyedfokú polinomok gyökei gyökjelekkel meghatározhatók (lásd megoldóképlet). Magasabb fokú polinomok nem oldhatók meg gyökjelekkel, ez az Abel-Ruffini-tétel.

A páratlan fokú valós együtthatós polinomoknak van legalább egy valós gyökük.

Az együtthatók és a fok alapján a gyökökre valós és komplex esetben is becslést lehet adni. Valós esetben a ${\displaystyle B\in \mathbb {R} _{+}}$ gyökkorlát, ha a polinom összes gyöke a ${\displaystyle [-B,B]}$ intervallumban található, vagyis a gyökök abszolút értéke nem nagyobb B-nél. B felső gyökkorlát, ha a polinom minden gyöke legfeljebb B. Hasonlóan definiálható az alsó gyökkorlát is.

A korlátokat normált, azaz 1 főegyütthatójú polinomokra adják meg; azonban mivel a nullától különböző konstanssal való szorzás (nullosztómentes esetben) nem változtatja meg a gyököket, a gyökök becsléséhez végig lehet osztani a főegyütthatóval. Legyen ekkor ${\displaystyle N=\left\{k\in \{0,1,\dotsc ,n-1\}\mid a_{k}<0\right\}}$ a negatív együtthatók halmaza. Ennek méretét a továbbiakban ${\displaystyle |N|}$ jelöli.

• Cauchy-szabály: egy felső gyökkorlát, ${\displaystyle B=\max \left\{\left.\left(|N|\cdot |a_{i}|\right)^{\frac {1}{n-i}}\right|i\in N\right\}}$
• Newton-szabály: egy felső gyökkorlát, ${\displaystyle B=\min\{x\in \mathbb {R} :f^{(i)}(x)\geq 0{\text{ minden }}i=0,\dotsc ,n\}}$
• Lagrange és Maclaurin szabálya: egy felső gyökkorlát, ${\displaystyle B=1+{\sqrt[{n-k}]{\alpha }}}$, ahol ${\displaystyle \alpha =\max\{|a_{m}|:a_{m}<0\}}$ a legnagyobb abszolút értékű negatív együttható abszolút értéke, és ${\displaystyle k=\max\{m:a_{m}<0\}}$ a legmagasabb kitevős negatív együttható kitevője.
• Minden ${\displaystyle B\in \mathbb {R} _{+}}$, amire teljesül, hogy ${\displaystyle B^{n}\geq \sum _{i=0}^{n-1}|a_{i}|B^{i}}$, gyökkorlát, ami a komplex gyökök abszolút értékét is behatárolja. Ennek speciális esetei Gerschgorin tételei:
  • ${\displaystyle B=1+\max \nolimits _{i=0,\,\dotsc ,\,n-1}|a_{i}|}$ és
  • ${\displaystyle B=\max \left(1,\sum _{i=0}^{n-1}|a_{i}|\right)}$.

Komplex gyökkorlátok esetén is a gyökök abszolútértékét határolják be. B komplex gyökkorlát, ha a polinom gyökei a nulla középpontú, B sugarú körben helyezkednek el. Egyes alkalmazásokban néhány, adott számú gyökre is értelmeznek gyökkorlátot.

Komplex gyökkorlát minden ${\displaystyle B\in \mathbb {R} _{+}}$, amire ${\displaystyle |a_{k}|B^{k}\geq \sum _{i\in \{0,\dotsc ,n\}\setminus \{k\}}|a_{i}|B^{i}}$ teljesül. Ekkor a nulla körüli, B sugarú kör pontosan k gyököt tartalmaz. Az egyenlet mindig megoldható ${\displaystyle k=0,n}$ esetén, de a közbenső számokra nem biztos. Ez Rouché tételének következménye. ${\displaystyle k=n}$ esetén a fent már említett egyenlet adódik. A ${\displaystyle k=0}$ eset egy gyököktől mentes körlapot ad. Ekkor ${\displaystyle 1/B}$ a reciprok polinom gyökkorlátja. Ha f polinom, akkor reciprok polinomja ${\displaystyle x^{n}f(1/x)/a_{0}}$.

Helyettesítési érték kiszámítása: a Horner-módszer

Bővebben: Horner-elrendezés

A gyökök meghatározása magasabb fok és irracionális gyökök esetén nem egyszerű; a Newton-módszerrel becsülhetők. Azt meghatározni azonban, hogy egy komplex szám gyöke-e egy adott polinomnak, létezik egy módszer, amit William George Horner angol matematikus dolgozott ki. A Horner-elrendezés arra is alkalmas, hogy segítsen a Newton-módszernek a polinom összes gyökének becslésében.

A módszer működésének megértéséhez vegyük észre, hogy a polinomok a következő alakban is felírhatók:

${\displaystyle p(x)=(\dots (a_{n}x+a_{n-1})x+\dots +a_{1})x+a_{0}}$

Tehát egy ${\displaystyle \,\!\alpha }$ komplex számról úgy tudjuk meg, hogy gyöke-e lesz-e a polinomunknak, hogy megnézzük a helyettesítési értékét az előző képlet szerint:

${\displaystyle p(\alpha )=(\dots (a_{n}\alpha +a_{n-1})\alpha +\dots +a_{1})\alpha +a_{0}}$

A módszer lényeges eleme az ún. Horner-séma lesz, azaz hogy ezt a fenti egyenletet táblázatba rendezzük azért, hogy a számolást meg tudjuk gyorsítani:

	${\displaystyle \,\!a_{n}}$	${\displaystyle \,\!a_{n-1}}$	${\displaystyle \,\!a_{n-2}}$	${\displaystyle \dots }$	${\displaystyle \,\!a_{0}}$
${\displaystyle \,\!\alpha }$	${\displaystyle \,\!a_{n}}$	${\displaystyle \,\!\alpha a_{n}+a_{n-1}}$	${\displaystyle \,\!\alpha (\alpha a_{n}+a_{n-1})+a_{n-2}}$	${\displaystyle \dots }$	${\displaystyle \,\!p(\alpha )}$

A fölső sorban a polinom együtthatói állnak. Az alsó sor első eleme a főegyüttható lesz, majd a következő tagokat úgy képezzük, hogy az előző tagot megszorozzuk ${\displaystyle \,\!\alpha }$-val majd hozzáadjuk a soron következő együtthatót. Így tehát az alsó sor elemei megfelelnek a fenti képlet egyes zárójeleinek, tehát végül ${\displaystyle \,\!a_{0}}$ alatt ${\displaystyle \,\!\alpha }$ helyettesítési értéke áll.

Megjegyzések:

1. A Horner-séma második sorában szereplő számok éppen az ${\displaystyle \,\!x-\alpha }$–val vett polinomosztás hányadosának együtthatói. Azaz ha egy gyököt megtaláltunk, szorzattá bonthatjuk a polinomunkat és az így kapott újabb polinomnak egy gyökét is próbálhatjuk megkeresni. Ezzel a módszerrel továbbhaladva eljuthatunk a polinom gyöktényezős alakjához.
2. Ha ${\displaystyle \,\!\alpha }$ helyettesítési értékére nem 0 jön ki akkor a kapott érték lesz az osztásunk maradéka.

Például vizsgáljuk meg, hogy a következő polinomnak gyöke-e a 3:

${\displaystyle \,\!x^{3}-5x^{2}+11x-15}$

A feladathoz tartozó Horner-séma:

	1	-5	11	-15
3	1	3${\displaystyle \cdot }$1-5=-2	3${\displaystyle \cdot }$(-2)+11=5	3${\displaystyle \cdot }$5-15=0

Tehát a 3 gyöke a polinomnak és az ${\displaystyle \,\!x-3}$ polinommal való leosztás után szintén a táblázatból leolvasva kapjuk, hogy a hányadospolinom az ${\displaystyle \,\!x^{2}-2x+5}$ lesz.

Gyökök és együtthatók közötti összefüggések

Bővebben: Viète-formulák

Legyenek a polinom együtthatói:${\displaystyle a_{n},a_{n-1},\dots a_{1},a_{0}}$, a gyökei pedig: ${\displaystyle x_{1},x_{2},\dots x_{n}}$. Ekkor a polinom gyökei és együtthatói között a következő összefüggések állnak fenn:

${\displaystyle {\frac {a_{0}}{a_{n}}}(-1)^{n}=x_{1}x_{2}\dots x_{n}}$

${\displaystyle {\frac {a_{1}}{a_{n}}}(-1)^{n-1}=(x_{1}\dots x_{n-1}+\dots +x_{2}\dots x_{n})}$

${\displaystyle \dots }$

${\displaystyle {\frac {a_{n-2}}{a_{n}}}(-1)^{2}=x_{1}x_{2}+x_{1}x_{3}+\dots +x_{n-1}x_{n}}$

${\displaystyle {\frac {a_{n-1}}{a_{n}}}(-1)=x_{1}+x_{2}+\dots +x_{n}}$

Ezeket az összefüggéseket Viète-formuláknak nevezzük. Előállításuk úgy történik, hogy ${\displaystyle \,\!p(x)}$ gyöktényezős alakjában elvégezzük a beszorzást és összevetjük az így kapott együtthatókat az általános felírásból adódókkal.

Másodfokú polinomokra így kapjuk meg a formulákat:

${\displaystyle \,\!p(x)=a_{2}x^{2}+a_{1}x+a_{0}=a_{2}(x-x_{1})(x-x_{2})}$

${\displaystyle \,\!a_{2}x^{2}+a_{1}x+a_{0}=a_{2}x^{2}-a_{2}x(x_{1}+x_{2})+a_{2}x_{1}x_{2}}$

Ezekből adódik tehát hogy:

${\displaystyle \,\!a_{1}=-a_{2}(x_{1}+x_{2})}$ és ${\displaystyle \,\!a_{0}=a_{2}x_{1}\cdot x_{2}}$

Analízis

A polinomok egyszerűen deriválhatók és integrálhatók:

${\displaystyle P(x)=a_{0}+a_{1}x+a_{2}x^{2}+\dotsb +a_{n}x^{n}=\sum _{i=0}^{n}a_{i}x^{i}}$

deriváltja

${\displaystyle {\begin{aligned}P'(x)&=a_{1}+2a_{2}x+3a_{3}x^{2}+\dotsb +na_{n}x^{n-1}\\&=\sum _{i=1}^{n}ia_{i}x^{i-1}=\sum _{i=0}^{n-1}(i+1)a_{i+1}x^{i}\,.\end{aligned}}}$

egy primtív függvénye

${\displaystyle {\begin{aligned}\int P(x)\,\mathrm {d} x&=a_{0}x+{\frac {1}{2}}a_{1}x^{2}+{\frac {1}{3}}a_{2}x^{3}+\dotsb +{\frac {1}{n+1}}a_{n}x^{n+1}\\&=\sum _{i=0}^{n}{\frac {a_{i}}{i+1}}x^{i+1}=\sum _{i=1}^{n+1}{\frac {a_{i-1}}{i}}x^{i}\,.\end{aligned}}}$

Ezek a műveletek sem vezetnek ki a polinomok közül.

Más függvények közelíthetők polinomokkal, például Taylor-sorral, interpolációval, Bernstein-polinomokkal.

A valós és a komplex polinomok hatványok lineáris kombinációi, ezért lassabban nőnek, mint bármely exponenciális függvény, aminek kitevője egynél nagyobb.

A páratlan fokú valós polinomok értékkészlete ${\displaystyle \mathbb {R} }$, azaz szürjektívek. Ha a főegyüttható pozitív, akkor ${\displaystyle -\infty }$-ből jönnek, majd ingadoznak egy szakaszon, utána ${\displaystyle +\infty }$-be mennek. Ha a főegyüttható negatív, akkor ${\displaystyle +\infty }$-ből jönnek, ingadoznak egy szakaszon, majd ${\displaystyle -\infty }$-be mennek.

A páros fokú polinomok értékkészlete pozitív főegyütthatóval ${\displaystyle \left[y_{\mathrm {min} },\,\infty \right[}$, és negatív főegyütthatóval ${\displaystyle \left]-\infty ,\,y_{\mathrm {max} }\right]}$. Menetük: pozitív főegyütthatóval ${\displaystyle +\infty }$-ből érkeznek, ingadoznak egy szakaszon, majd ${\displaystyle +\infty }$-be mennek. Negatív főegyütthatóval ${\displaystyle -\infty }$--ből jönnek, ingadoznak egy szakaszon, majd ${\displaystyle -\infty }$-be mennek.

A polinomok végtelen sorok formájában függvények közelítésénél is használatosak. Ekkor a függvényeket Taylor-sorba fejtve kapunk hozzájuk határértékben tartó hatványsorokat. Ha ezeknek a végtelen soroknak csak véges alakjait tekintjük, akkor beszélünk Taylor-polinomokról.

Két a racionális számok teste feletti polinom hányadosát racionális függvénynek vagy racionális törtfüggvénynek hívjuk. Ezeknek az integrálása az integrálszámítás egyik alapváltozata. A művelet elvégzéséhez a parciális törtekre bontás módszerét szükséges alkalmazni.

Interpoláció

Az interpoláció módszerének segítségével ${\displaystyle \,\!n}$ különböző komplex számpárra, vagyis ${\displaystyle n}$ pontra a komplex számsíkon egyértelműen illeszthető (n–1)-edfokú polinom, amely áthalad a megadott pontokon.

Bizonyítás

Legyenek az adott pontpárok a következők: ${\displaystyle (x_{1},y_{1}),(x_{2},y_{2}),\dots (x_{n},y_{n})}$. Először az egyértelműséget igazoljuk. Ha ${\displaystyle \,\!p(x)}$ és ${\displaystyle \,\!q(x)}$ két a feltételeknek eleget tevő polinom, akkor ${\displaystyle \,\!p(x)-q(x)}$ egy olyan legfeljebb (${\displaystyle \,\!n-1}$)-ed fokú polinom, amelynek ${\displaystyle x_{1},x_{2},\dots ,x_{n}}$ gyöke. Az algebra alaptétele szerint ez csak akkor lehetséges, ha ${\displaystyle p(x)-q(x)\equiv 0}$, vagyis ${\displaystyle \,\!p(x)=q(x)}$.

Most konstruáljunk meg egy ilyen polinomot Lagrange módszerével. Ehhez konstruáljuk meg az ún. Lagrange-féle alappolinomokat:

${\displaystyle l_{i}(z)={\frac {(z-x_{1})\dots (z-x_{i-1})(z-x_{i+1})\dots (z-x_{n})}{(x_{i}-x_{1})\dots (x_{i}-x_{i-1})(x_{i}-x_{i+1})\dots (x_{i}-x_{n})}}=\prod _{j=1}^{n}{\frac {(z-x_{j})}{(x_{i}-x_{j})}}}$

Ezekre ${\displaystyle \,\!l_{i}(x_{i})=1}$ és ${\displaystyle \,\!l_{i}(x_{j})=0}$, ha ${\displaystyle i\neq j}$.

Tehát a ${\displaystyle p(z)=\sum _{i=1}^{n}y_{i}l_{i}(z)}$ polinom teljesíti a feltételeket.

Példa

Legyenek a pontok a következők: (-1;1), (0;2), (1;4); ekkor ezek lesznek a Lagrange-féle alappolinomok:

${\displaystyle l_{1}(x)={\frac {(x-0)(x-1)}{(-1-0)(-1-1)}}={\frac {1}{2}}(x^{2}-x)}$

${\displaystyle l_{2}(x)={\frac {(x+1)(x-1)}{(0+1)(0-1)}}=-1(x^{2}-1)}$

${\displaystyle l_{3}(x)={\frac {(x+1)(x-0)}{(1+1)(1-0)}}={\frac {1}{2}}(x^{2}+x)}$

Ekkor a feltételeket kielégítő polinom ez lesz:

${\displaystyle p(x)=1\cdot \left({\frac {1}{2}}(x^{2}-x)\right)+2\cdot (-1(x^{2}-1))+4\cdot \left({\frac {1}{2}}(x^{2}+x)\right)={\frac {1}{2}}x^{2}+{\frac {3}{2}}x+2}$

Általánosítások

A hatványsorok alakja:

${\displaystyle f=\sum _{i=0}^{\infty }a_{i}X^{i}}$

Ha nem foglalkozunk a konvergenciával, akkor a hatványsor formális, ami nem mindig állít elő függvényt. Ha egy bizonyos tartományon (nemcsak egy pontban) konvergens, és előállítja a függvényt, akkor egy analitikus függvényhez jutunk, amit újra vizsgálni lehet.

A Laurent-sorok alakja:

${\displaystyle f=\sum _{i=-N}^{\infty }a_{i}X^{i}.}$

A Laurent-sorok a hatványsorokhoz hasonlóan vizsgálhatók.

Ha az összeg véges, de a monomokban tetszőleges valós hatványkitevőket megengedünk, akkor poszinomiális függvényekhez jutunk.

További információk

• Alice és Bob - 26. rész: Alice és Bob átlépi a célvonalat

Jegyzetek

Források

• Horváth Erzsébet: Lineáris algebra (Műegyetemi Kiadó, 2002)
• Konsztantyin Alekszejevics Ribnyikov: A matematika története (Tankönyvkiadó, Budapest, 1968)
• Nagy Attila (BME-TTK) Lineáris algebra c. előadásai
• Beutelspacher: Lineare Algebra. 6. Auflage.
• Holz, Wille: Repetitorium der Linearen Algebra, Teil 2.
• Gerd Fischer: Lehrbuch der Algebra.

Fordítás

Ez a szócikk részben vagy egészben a Polynom című német Wikipédia-szócikk fordításán alapul. Az eredeti cikk szerkesztőit annak laptörténete sorolja fel. Ez a jelzés csupán a megfogalmazás eredetét és a szerzői jogokat jelzi, nem szolgál a cikkben szereplő információk forrásmegjelöléseként.