Longueur d'un arc
Pour un article plus général, voir Périmètre.

En géométrie, la question de la longueur d'un arc est simple à concevoir (intuitive). L'idée d'arc correspond à celle d'une ligne, ou d'une trajectoire d'un point dans un plan ou l'espace par exemple. Sa longueur peut être vue comme la distance parcourue par un point matériel suivant cette trajectoire ou encore comme la longueur d'un fil prenant exactement la place de cette ligne. La longueur d'un arc est, soit un nombre positif, soit l'infini.
Un vieil exemple est celui du demi-cercle de rayon r, où r désigne un nombre réel positif. Sa longueur est égale à πr. Un exemple, plus simple, est donné par un segment, sa longueur est égale à la distance qui sépare ses deux extrémités.
Selon l'époque, différentes méthodes permettent de définir et de mesurer la longueur d'un ensemble d'arcs de plus en plus vaste. Eudoxe de Cnide, un mathématicien grec du IVe siècle av. J.-C., puis Archimède utilisent une méthode, dite d'exhaustion pour calculer celle d'un arc de cercle. La physique de la fin du XVIIe siècle développe une nouvelle approche, fondée sur les progrès réalisés en mécanique du point grâce en particulier au calcul infinitésimal appliqué à l'astronomie. La longueur d'un arc est perçue comme le produit du temps nécessaire à un point matériel pour parcourir l'arc par sa vitesse, si elle est supposée constante. Cette définition est généralisée par Bernhard Riemann et devient la pierre angulaire pour construire une distance et de nouvelles formes de géométries, sur des objets maintenant appelés variétés riemanniennes.
Pour le mathématicien français Camille Jordan (1838 - 1922), ces définitions sont trop restrictives. Il s'intéresse aux propriétés d'une courbe fermée, c'est-à-dire un arc dont le point initial se confond avec le point final. La définition précédente, issue de la physique deux siècles plus tôt, suppose que l'arc soit dérivable. Cette limitation empêche l'usage d'un vaste arsenal de méthodes, pourtant indispensables à la résolution de nombreuses questions. Il propose une nouvelle définition, à l'aide d'une borne supérieure et de la longueur d'une ligne polygonale. C'est maintenant la plus communément utilisée. Pour Hermann Minkowski (1864-1909), les idées de Jordan sont peu adaptées à ses besoins. Dans le contexte des questions qu'il se pose, la longueur qu'il cherche à définir est surtout celle de la frontière d'une surface. Un cercle est défini comme l'ensemble des points P d'un disque tels que tout voisinage de P contient un point du disque et un point extérieur. Il définit la longueur à l'aide de la notion intuitive de tube, correspondant à l'ensemble des points situés à une distance inférieure à r d'un point de l'arc. Cette définition se prête à de nombreuses généralisations, qui permettent même de donner un sens à la longueur d'une courbe fractale.
Premiers calculs

L'une des mesures de longueur la plus célèbre et la plus ancienne est celle d'un demi-arc de cercle de rayon 1. Cette longueur, notée π est calculée depuis bien longtemps. Pour les babyloniens, sa valeur se calcule grâce à la relation qui relie l'aire du cercle avec le périmètre du demi-arc, ils trouvent l'approximation 3 + 1/8[1].
Un progrès théorique important est l'œuvre d'Archimède[2]. Pour le physicien, un polygone convexe dont les sommets sont des points du cercle est de périmètre plus petit que celui du cercle. En effet, il est plus court, pour rejoindre deux sommets consécutifs de passer par l'arête (le segment est le plus court chemin entre ses deux points d'extrémités), ce qui donne une minoration de π. Inversement, le polygone convexe régulier dont chaque milieu d'arête est un point du cercle est de périmètre plus grand. S'il ne peut démontrer cette proposition en général car il ne dispose pas d'une définition de la longueur d'un arc qui lui permettrait de réaliser cette prouesse, elle semble intuitive à l'œil, et résulte (dans le cas du cercle) de la proportionnalité entre les aires de secteurs circulaires et les arcs qui les sous-tendent. À l'aide d'un polygone régulier de 96 côtés, il démontre que la valeur de π se situe entre 3 + 1/7 et 3 + 10/71. Le principe du calcul est donné dans l'article pi.
La méthode est générale pour tout arc dont la convexité se situe toujours du même côté, c'est-à-dire dont l'arc n'est composé que de points frontières de l'enveloppe convexe. Toute ligne polygonale, dont les sommets sont situés sur l'arc, possède une longueur plus petite que celle de l'arc étudié. On dispose ainsi d'un minorant. On peut alors construire une suite de lignes polygonales de longueurs croissantes (pn) toutes plus petites que la longueur de l'arc. On construit ensuite une suite de lignes polygonales à l'extérieur de l'enveloppe convexe, dont les extrémités sont ceux de la ligne polygonale et qui longent de plus en plus précisément l'arc. La suite des longueurs (Pn) est choisie décroissante et chaque longueur est plus grande que celle de l'arc. Les seules valeurs possibles, pour la longueur de l'arc, sont situées dans le segment [pn, Pn]. La suite est construite de manière que la distance entre pn et Pn soit de plus en plus petite à tel point que pour tout nombre strictement positif ε, il existe une valeur n tel que Pn – pn soit strictement plus petit que ε. L'intersection de tous les intervalles [pn, Pn] est réduite à un point, qui est nécessairement la longueur de l'arc. Cette méthode est dite d'exhaustion.
Elle est utilisée par le mathématicien chinois Liu Hui durant le IIIe siècle avec des approximations plus performantes que celles d'Archimède. Il trouve la valeur approchée de π égale à 3,1416[3]. Cette méthode reste en vigueur jusqu'à la fin du XVIIe siècle et permet de trouver d'autres résultats comme la longueur d'un arc de spirale logarithmique par Torricelli[4] en 1645 ou de cycloïde par Christopher Wren[5].
Arc de classe C1
Une approche cinématique
Le XVIIe siècle est celui de Galilée. La notion de vitesse instantanée prend un sens, et même deux. La vitesse est tout d'abord un vecteur, celui qu'il faut multiplier par une durée a pour connaître la position d'un point se déplaçant de manière rectiligne uniforme au bout d'un délai a. C'est aussi un scalaire, celui qui indique la distance parcourue au bout de la durée a, dans le cas d'un déplacement uniforme. On parle de vitesse curviligne pour différencier cette grandeur de la vitesse vectorielle. La vitesse curviligne correspond à la norme du vecteur vitesse. Souvent, le terme de vitesse, utilisé dans le langage courant, correspond à la vitesse curviligne, par exemple dans l'expression vitesse de 80 km/h, qui correspond à un scalaire et non à un vecteur.
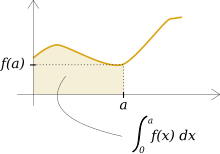
Cette définition permet une nouvelle manière d'appréhender la longueur d'un arc. Pour connaître cette longueur, il suffit de trouver une fourmi, supposée petite, se déplaçant toujours à une vitesse curviligne f constante, de lui faire parcourir l'arc. Si la durée du parcours de l'arc est égale à a, alors sa longueur est a.f. Si cette idée est fructueuse, elle demande à être aménagée. Modéliser le parcours d'un arc à vitesse constante est une question souvent plus difficile que le calcul de la longueur recherchée. Si la vitesse f est constante, la longueur peut être vue comme la surface d'un rectangle de longueur le temps a, nécessaire pour parcourir l'arc et de hauteur f. Si la vitesse n'est pas constante, on remplace la droite y = f dans un repère cartésien par la ligne d'équation y = f(t), où t varie entre 0 et a. La longueur de l'arc est égale à l'aire située entre les trois droites x = 0, x = a, y = 0 et la ligne y = f(t). On trouve l'aire illustrée en jaune sur la figure de droite.
Cette nouvelle approche prend forme à travers l'étude de la parabole semi-cubique[6], d'équation cy2 = x3. Vers 1660, ce problème est célèbre et intéresse de nombreux mathématiciens. La question du calcul de la longueur d'un arc, que l'on appelait alors problème de rectification, était à l'époque considérée comme très difficile, voire souvent impossible. John Wallis publie la solution[7] en 1659 et en attribue la paternité à Neil. Une des raisons de la célébrité de la preuve est qu'elle débouche sur une valeur constructible à la règle et au compas, naissance d'un fol espoir de résolution de la quadrature du cercle. Cette solution est reproduite par Van Heuraet la même année avec une méthode de rectification de la parabole à l'aide du calcul de la quadrature d'une hyperbole[8]. Le problème de la quadrature d'une surface est celui consistant à déterminer son aire. En 1660, Pierre de Fermat généralise l'approche à toute courbe, qu'à l'époque on imagine comme toujours dérivable, au moins par morceau, même si la notion de dérivée n'est pas encore formalisée[9].
Un pas de géant est franchi entre 20 et 30 ans plus tard, lorsque Isaac Newton et Gottfried Wilhelm Leibniz découvrent le calcul infinitésimal et le second théorème fondamental de l'analyse, indiquant la relation entre la dérivée et l'intégrale. La longueur L d'un arc parcouru durant une période a à une vitesse curviligne égale à f(t) à l'instant t est égale à :
Définitions
Pour être précis, quelques définitions doivent être données. Ici, E désigne un espace euclidien de dimension n et ℝ l'ensemble des nombres réels. Pour définir une longueur, il est utile d'associer un sens précis au mot arc paramétré de classe Cp, si p est un entier positif :
Définition d'un arc paramétré — Un arc paramétré de classe Cp est un couple (I, f) composée d'un intervalle I de ℝ et d'une fonction de I dans un espace euclidien, p fois dérivable, dont la dérivée pième est continue et dont la dérivée première ne s'annule jamais[10].
Demander à la dérivée première de ne jamais s'annuler permet d'éviter des singularités qui ne sont pas l'objet de cet article. Cette définition fournit à la fois l'arc et une manière de le parcourir. Pourtant, géométriquement, parcourir un arc rapidement ou lentement, dans un sens ou dans un autre, ne modifie pas la nature de l'arc. Pour cette raison, on définit une classe d'équivalence entre les arcs paramétrés :
Définition d'arcs Cp-équivalents — Soient (I, f) (J, g) deux arcs paramétrés à valeurs dans E. S'il existe un difféomorphisme θ de classe Cp de I dans J tel que g∘θ soit égal à f on dit que les deux arcs paramétrés sont Cp-équivalents[11].
Par exemple, le parcours deux fois d'un cercle par un arc paramétré n'est jamais équivalent à un arc paramétré parcourant une seule fois le cercle. En effet, dans un cas tout point du cercle possède deux antécédents et dans l'autre cas un unique, un difféomorphisme ne peut exister. On peut maintenant énoncer la définition d'un arc géométrique :
Définition d'un arc géométrique de classe Cp — Un arc géométrique est une classe d'équivalence d'arcs Cp-équivalents[11].
Il devient possible de définir rigoureusement la longueur d'un arc géométrique[12] :
Définition de la longueur d'un arc géométrique de classe Cp — La longueur d'un arc géométrique ayant pour représentant (I, f) est la valeur L de l'intégrale suivante, égale à un nombre positif ou à l'infini :
L'intégrale n'est pas nécessairement finie car l'intervalle I n'est pas nécessairement un segment. Par exemple, si I est égal à ℝ et f à la fonction qui à t associe exp(it) à valeurs dans les nombres complexes identifiés au plan euclidien, l'arc géométrique parcourt un nombre infini de fois le cercle unité, sa longueur est infinie.
Pour que la définition ait du sens, il est nécessaire que les longueurs de deux arcs Cp équivalents soient les mêmes. On le vérifie simplement. Si (I, f) et (J, g) sont deux arcs paramétrés Cp équivalents et si le difféomorphisme θ vérifie g∘θ = f, alors l'intégration par changement de variable montre que :
Formulation

Si E désigne un plan euclidien, la fonction f peut s'exprimer à l'aide de deux fonctions coordonnées, de I dans ℝ, notées ici x(t) et y(t). Si les coordonnées s'expriment dans une base orthonormale et si ]a, b[ désigne l'intervalle I, la formule précédente devient :
Sous cette forme, la longueur de l'arc trouve une autre justification intuitive que celle de la vitesse. Soit t et dt deux réels positifs tel que t et t + dt soient éléments de I. Notons (x, y) les coordonnées de l'image de t et (x + dx, y + dy) celle de t + dt. Cette situation est illustrée sur la figure de droite. Si dt est suffisamment petit, la courbe est proche de son approximation tangente. Identifier entre ces deux valeurs du paramètre l'arc avec son approximation linéaire tangente au point t ramène localement le calcul à celui de la longueur ds de l'hypoténuse d'un triangle rectangle, qui se calcule avec le théorème de Pythagore :
Il existe un cas particulier usuel, celui où la courbe est le graphe d'une fonction g de classe C1 sur un intervalle I et à valeurs dans ℝ. Pour revenir à une situation plus proche de la précédente, on peut considérer que la courbe est représentée par l'arc paramétré (I, f) où f est la fonction de I dans ℝ2 qui à t associe (t, g(t)). En supposant toujours que ]a, b[ désigne l'intervalle I, on obtient :
Il est parfois plus commode d'utiliser les coordonnées polaires pour exprimer l'arc paramétré, ce qui revient à utiliser les notations suivantes :
On en déduit :
ce qui permet d'établir la formule :
En dimension 3 et sous les mêmes hypothèses, la formule prend la forme :
Exemples
Sur le cercle trigonométrique, la longueur de l'arc ayant pour extrémités l'origine des arcs et le point du premier quadrant d'ordonnée est :

Au XVIIe siècle, le problème de la rectification d'un arc est à la pointe de la recherche. Sans les outils du calcul différentiel, ces questions demandent une grande imagination pour y répondre. Elles deviennent beaucoup plus aisées une fois connue la dérivée et sa relation avec l'intégrale. Un exemple est celui de la chaînette, courbe plane qui correspond à la forme que prend un câble lorsqu'il est suspendu par ses extrémités et soumis à son propre poids. Il est résolu en 1691 à la fois par Leibniz, Huygens et les frères Bernoulli[13]. Si cosh désigne le cosinus hyperbolique et si a désigne un réel strictement positif, son équation est la suivante :
La longueur L0 de la chaînette entre le point d'abscisse 0 et celui d'abscisse x0 est donnée par la formule, si sinh désigne le sinus hyperbolique :

La longueur d'une spirale logarithmique est d'abord déterminée sans l'usage du calcul différentiel. Puis, cet usage permet une résolution du problème de manière très simple, surtout si le paramétrage proposé est polaire si a est un réel strictement positif et b est strictement supérieur à 1 :
La longueur Lθ de la spirale entre le point origine et celui d'angle θ, qui peut être supérieur à 2π, est donnée par la formule suivante :

Un autre calcul est d'importance historique, celui de la parabole de Neil, qui correspond à la courbe d'équation y = ±ax3/2, si a est un entier strictement positif. Sa rectification est réalisée avant la découverte du calcul différentiel. La nouveauté apportée réside dans le fait que, si L0 désigne la longueur de la partie positive de la branche située entre 0 et x0, le résultat intermédiaire suivant est utilisé :
Une question de rectification est finalement liée à un problème de quadrature, c'est-à-dire au calcul d'une surface, base de la définition utilisée dans ce paragraphe. Finalement, on trouve :
Cette démarche permet de résoudre le problème de la rectification de la parabole. Si l'on choisit le paramétrage y = ax2, avec a un réel strictement positif, la longueur L0 de la branche située entre 0 et x0 s'exprime sous la forme d'une quadrature d'hyperbole, que l'on sait réaliser déjà depuis plus de 20 ans :
Si l'approche par la vitesse permet de résoudre aisément la question de la longueur de l'arche d'une cycloïde, égale à 8 fois le rayon du cercle, un problème en apparence aussi simple que de calculer la circonférence de l'ellipse en fonction des demi-axes conduit à des intégrales qu'on ne peut pas expliciter plus avant : on parle d'intégrales elliptiques de seconde espèce.
Les calculs sont analogues en dimension 3. L'article « Loxodromie » explicite un exemple.
- Rectification du cercle trigonométrique :
On utilise la paramétrisation par les fonctions et définies sur :
Leurs dérivées sont :
D'où :
- Rectification de la chaînette :
On utilise ici la paramétrisation par une fonction g, définie par g(x) = acosh(x/a). On obtient les expressions :
On en déduit :
- Rectification de la spirale logarithmique :
À l'aide des coordonnées polaires, on obtient :
On en déduit :
- Rectification de la parabole de Neil :
L'arc est paramétré par la courbe y = g(x), ce qui amène le calcul :
puis, en utilisant le changement de variable u = 9a2x/4 :
- Rectification de la parabole :

La rectification de la parabole est un peu plus subtile. Avec les notations précédentes :
On en déduit :
L'aire à déterminer est illustrée sur la figure de droite. Elle est comprise entre les deux droites d'équations x = 0 et x = τ, puis entre la droite y = 0 et la fonction dont l'équation est sous l'intégrale. Sans disposer des outils puissants de l'analyse, il est possible de calculer cette aire. On la découpe en trois zones, la jaune, la bleue et la vert clair.
La zone jaune correspond à un demi-carré de côté 1, la bleue à un demi-carré de côté τ. Déterminons la surface vf du triangle vert foncé. Pour cela, il suffit de calculer la longueur de sa diagonale vd :
Il reste encore à déterminer l'aire de la zone vert clair vc, elle est égale à la différence entre l'aire de zone verte v et de la zone vert foncé. La zone verte correspond au logarithme de la distance qui sépare l'origine du sommet du triangle vert foncé le plus éloigné, on trouve :
On en déduit :
ce qui montre que, si √2μ = τ :
- Rectification de la cycloïde :
Un paramétrage usuel de la cycloïde de rayon a est le suivant :
Ce paramétrage permet le calcul de la norme de la dérivée :
La longueur recherchée est :
Géométrie différentielle
Principe de Fermat


Pierre de Fermat est un des précurseurs du calcul différentiel, avant Leibniz et Newton. Il propose une interprétation des lois de Snell-Descartes dans une lettre de 1662 et adressée à Marin Cureau de la Chambre en énonçant un principe très général : « la nature agit toujours par les voies les plus courtes[14] » qui implique les règles de propagation de la lumière pour l'optique géométrique.
L'intuition de Fermat est exacte. La vitesse de la lumière est plus lente dans l'eau ou dans du verre que dans le vide ou dans l'air. La trajectoire de la lumière est en conséquence fonction du rapport des vitesses de la lumière dans les deux milieux. Il est possible d'illustrer ce principe par le problème dit du maître nageur, représenté sur la figure de gauche. Un maître nageur, situé au point A1 doit éviter une noyade en A2. Pour être le plus rapide possible, le maître-nageur doit trouver le point M situé à la frontière entre la plage et la mer tel que courir de A1 à M, puis nager de M à A2, soit le trajet le plus rapide. Comme il court plus vite qu'il ne nage, le point M se trouve nécessairement plus proche de A2 que le point du segment A1A2 à la frontière de la plage et de la mer.
Une autre manière de modéliser cette question est d'équiper l'espace d'une nouvelle distance d2, associée à la vitesse de déplacement de la lumière ou de celle du maître-nageur. La distance entre deux points est donnée par le temps nécessaire pour aller d'un point à un autre. Si C est un arc géométrique de paramétrage (I, f), et nA le rapport entre la vitesse du maitre nageur sur la plage et celle au point A, la longueur de l'arc C s'exprime par :
C'est maintenant la longueur d'un arc qui permet de définir la distance d2 : la distance entre deux points est la plus petite longueur d'un arc reliant ces deux points. La figure de droite illustre la géométrie de l'espace, vue avec les deux distances. L'espace équipé de la distance d2 est illustré en haut. Les trajectoires les plus courtes pour le maitre nageur sont les droites représentées en vert, et les points à égale distance de sa position sont les arcs de cercle, en rouge sur la plage et en bleu dans la mer. Cette même figure est reproduite sur la figure du bas, cette fois avec la distance usuelle. Comme le maître nageur est moins rapide dans l'eau, les portions de cercles dans la mer sont écrasées. Ce tassement déforme les portions de droites vertes qui se trouvent dans l'eau. Les angles obtenus, entre un segment vert sur la plage et son prolongement dans l'eau, suivent les lois de Descartes[15].
Principe de moindre action

L'expression utilisée par Fermat pour décrire son principe est habile. Rien n'indique, dans sa formulation, qu'il est limité à l'optique géométrique. L'avenir lui donne raison. Une question, déjà abordée par Galilée sans succès en 1638[16], consiste à trouver la courbe que doit emprunter un point matériel glissant sans frottement pour aller le plus rapidement possible d'un point A à un point B. Le point B est supposé se trouver à une altitude inférieure ou égale à celle du point A pour que la question ait une solution. Cette question porte le nom de problème brachistochrone. Elle est remise à l'honneur par Jean Bernoulli en 1696 et posée comme défi aux lecteurs du journal Acta Eruditorum[17].
Une solution consiste encore à appliquer le principe de Fermat. Si la distance entre deux points A et B est mesurée par le temps nécessaire pour aller du plus haut au plus bas, l'espace est cette fois dilaté de manière parabolique sur l'axe vertical. En effet, si on appelle 1 la longueur parcourue verticalement en 1 unité de temps, la longueur parcourue verticalement en 2 unités de temps est de 4, puis celle parcourue en 3 est de 9, etc. Résoudre le problème brachistrochrone revient à trouver les lois de passage entre l'espace mesuré par la vitesse du point matériel et celui mesuré de la manière usuelle. La réponse est illustrée sur la figure de droite. Comme précédemment la figure du dessus représente l'espace mesurée à l'aide de la distance d2, correspondant à la vitesse du point matériel. On considère les trajectoires, vues avec la distance d2 comme des demi-droites issues d'un même point, où la vitesse du point est initialement nulle. Ces demi-droites sont régulièrement espacées d'un angle de π/8 sur la figure. En rouge sont indiquées les positions possibles du point au bout d'un temps fixe et régulier, 1, 2, 3 et 4 secondes. Les courbes rouges correspondent à ce que l'on appelle usuellement des demi-cercles.
Cette même figure, vue avec la distance usuelle est illustrée sous la première. Elle est un peu plus difficile à lire que celle correspondant à la géométrie précédente. Le plus simple est de commencer par la ligne verte numérotée 1. Elle correspond à un déplacement horizontal. Comme le point matériel possède une vitesse initiale nulle, son déplacement est nul et la droite est transformé en un point, noté 1 sur la figure du bas. La trajectoire noire correspond à une courbe dont la tangente initiale est verticale. Il n'existe pas une courbe possible, mais une infinité, dont deux sont illustrées sur la figure du bas, en noir. Ces courbes correspondent à des arches complètes de cycloïde. Toute arche de cycloïde de point initial celui de la figure correspond à une droite de tangente initiale verticale avec la distance d2. Cette situation est analogue pour l'image de toutes les demi-droites vertes de la figure supérieure. Ainsi, la demi-droite numéroté 2 correspond à une portion de cycloïde illustrée sur la partie basse de la figure, et toute homothétie de cette portion de cycloïde correspond aussi à une image de la demi-droite 2.
La technique utilisée pour résoudre le problème brachistochrone est de même nature que celle du paragraphe précédent en optique. On cherche l'arc le plus court pour une distance bien choisie. Le principe de Fermat prend parfois le nom de principe de moindre action, que Maupertuis redécouvre et énonce ainsi : « L'Action est proportionnelle au produit de la masse par la vitesse et par l'espace. Maintenant, voici ce principe, si sage, si digne de l'Être suprême : lorsqu'il arrive quelque changement dans la Nature, la quantité d'Action employée pour ce changement est toujours la plus petite qu'il soit possible[18]. »
Variété riemannienne

Dans l'exemple du problème brachistochrone, l'équivalent de l'indice de réfraction correspond un facteur de compression de l'espace, à l'image de l'exemple d'optique. Comme ici l'espace a plutôt tendance à se dilater, l'indice est rapidement compris entre 0 et 1. Il est précisément égal à (2gh)-1/2 si h est l'altitude, comptée négativement. Pour résoudre l'équation différentielle de Newton, indiquant la trajectoire des planètes, la même méthode s'applique avec un coefficient cette fois ci, égal à a/h. Les calculs sont un peu plus simples et les arches de cycloïdes sont transformées en demi-cercles.

Si Bernhard Riemann, un élève de Gauss, s'intéresse suffisamment à cette question pour en faire son sujet de thèse[19], ce n'est pas pour proposer une nouvelle méthode de résolution d'une célèbre équation différentielle, mais pour mieux comprendre la géométrie. Si l'on retire les points d'altitude 0 (un point d'altitude 0 est en effet à une distance non nulle de lui-même, ce qui ne fait guère sens), on obtient un espace métrique. Pour définir cette métrique, on commence par une nouvelle définition de la longueur LC d'un arc C de l'espace G qui, s'il est paramétré par (I, f) vaut dans le cas particulier étudié :
Chaque point p de G possède un espace tangent Tp, muni d'un produit scalaire et donc d'une norme. Dans le cas particulier du paragraphe, la norme est celle du plan, que multiplie le facteur de compression np proportionnel à l'inverse de l'altitude de p. La définition de la longueur d'un arc permet ensuite de définir la distance entre deux points. Elle est égale à la longueur du plus petit arc reliant ces deux points.
Qualitativement, l'espace que l'on vient de définir ressemble un peu à la figure de droite. Le formalisme de Riemann, consistant à d'abord définir la longueur d'un arc puis la distance, est finalement très puissant. Il permet de définir un large ensemble de géométries, dans lequel les concepts classiques comme les droites (qui prennent le nom de géodésiques), les cercles ou les courbures s'étendent. Cette méthode permet de définir des surfaces qui n'existent pas en dimension 3. Celle considérée dans ce paragraphe possède une courbure constante négative. La courbure en un point p correspond au produit des deux courbures les plus extrêmes que peuvent prendre les arcs paramétrés à l'aide d'une abscisse curviligne au point p. Si les deux cercles osculateurs se trouvent sur un ellipsoïde, on parle de courbure positive. s'ils se trouvent sur une selle de cheval, on parle de courbure négative. Aucune surface en dimension 3 ne possède de courbure négative constante, raison pour laquelle la géométrie décrite dans ce paragraphe n'est pas exactement celle de la figure de droite[20].
Calcul des variations
Les trois paragraphes précédents ont un point commun, pour être opérationnel, ils nécessitent la capacité de trouver le plus court chemin entre deux points d'une surface ou d'une géométrie particulière, ce qui n'est pas, en général, une question facile.


La méthode la plus fructueuse s'apparente à celle de la géométrie différentielle. En dimension finie, et sous les bonnes hypothèses, un point optimal possède une approximation linéaire tangente plate, illustrée sur la figure de gauche. En terme mathématiques, cela signifie que le gradient de la fonction à optimiser est nul sur un point extrémal.
C'est une méthode de cette nature qu'utilise Bernoulli pour résoudre le problème brachistochrone. Elle est illustrée sur la figure de droite, une petite variation autour du chemin optimal ne change pas sa longueur, au premier ordre. Ainsi le chemin proche de l'optimal, illustré en vert, est au premier ordre, de même longueur que la courbe optimale, illustrée en gris. Leonhard Euler affine la méthode et propose une première démonstration de la résolution du problème isopérimétrique[21] consistant à trouver l'arc fermé d'une longueur donnée et enserrant une surface de plus grande aire possible. (La démonstration d'Euler est proposée dans l'article Multiplicateur de Lagrange.) En 1755, Lagrange écrit une lettre à Euler. Elle porte sur le calcul de la courbe tautochrone, correspondant à une question analogue au problème brachistochrone[22]. Cette correspondance est le début d'un long travail commun et permet d'établir l'équation d'Euler-Lagrange, une méthode très générale pour trouver les géodésiques.
Si l'équation d'Euler-Lagrange est suffisante pour résoudre le problème tautochrone, il est parfois nécessaire de l'enrichir, par exemple pour trouver la courbe de la chaînette, c'est-à-dire la position qu'occupe au repos un câble de densité linéaire (les physiciens emploient l'expression masse linéique) constante, soumis à la gravité. La méthode est enrichie par celle du multiplicateur de Lagrange.
Les mathématiques du XVIIIe siècle sont encore insuffisantes pour démontrer rigoureusement la pertinence des calculs d'Euler et de Lagrange. Leur connaissance en analyse fonctionnelle est encore bien trop limitée. Ces méthodes, qui prennent le nom de calcul des variations, deviennent vraiment rigoureuses sous l'influence de Karl Weierstrass au XIXe siècle et surtout les travaux de Banach et Sobolev au XXe siècle.
Espace de Sobolev
Posons la question en termes flous : deux courbes « proches » ont-elles des longueurs voisines ?
Voici un exemple négatif. On prend le graphe de la fonction constante égale à 0 sur [0, 1]. Celui-ci est de longueur 1. On fabrique facilement une suite de fonctions continues sur [0, 1], rectifiables, qui converge uniformément vers f et dont la longueur ne converge pas vers 1.
Par exemple : f1 est une fonction triangle avec des pentes 1 sur [0, 1/2] et –1 sur [1/2, 1]. Puis f2 est une fonction formée de deux triangles, avec des pentes 1 sur [0, 1/4], –1 sur [1/4, 1/2], 1 sur [1/2, 3/4], –1 sur [3/4, 1], et ainsi de suite (4,8,16 triangles…). Chacune des fonctions fn a un graphe de longueur √2, et par ailleurs il y a bien convergence uniforme vers f.
Pour obtenir des résultats de continuité pour l'application « longueur », il ne faut donc pas travailler avec la norme de la convergence uniforme. Il faudrait plutôt une norme du type de celles des espaces de Sobolev.
Définition de Jordan
Motivation
Pendant 150 ans, la définition du XVIIe siècle remplit les besoins des mathématiciens, au besoin avec la généralisation de Riemann. Encore maintenant, il n'est pas rare qu'elle soit utilisée[23] quand le sujet se limite à de la géométrie différentielle. Durant la deuxième moitié du XIXe siècle, de nouvelles questions imposent une approche plus générale.
Les courbes étudiées ne possèdent plus systématiquement une origine spécifiquement mécanique ou cinématique mais proviennent aussi d'autres branches des mathématiques. Giuseppe Peano découvre[24] la courbe qui porte maintenant son nom et qui recouvre intégralement la surface d'un carré de côté 1. Hermann Minkowski utilise des convexes pour résoudre des questions de théorie algébrique des nombres[25]. Les frontières de ces convexes, s'ils sont dans un plan euclidien, peuvent parfois être paramétrées comme des arcs.

Camille Jordan est un précurseur dans l'étude des courbes du plan euclidien ayant une autre origine que cinématique. Il essaie de résoudre certaines questions apparemment anodines comme celle du théorème portant son nom, ce résultat traite d'une courbe fermée et simple. Fermée signifie que l'image des extrémités du segment de définition sont confondues et simple que l'unique point double est l'extrémité. Une telle courbe sépare le plan en deux parties connexes, l'intérieur et l'extérieur de la courbe.
Pour supporter un tel développement, il est nécessaire de ne pas se limiter aux arcs géométriques de classe C1. Jordan propose une nouvelle définition de la longueur[26] fondée sur une démarche plus proche de celle d'Archimède que des analystes du XVIIe siècle. Une méthode intuitive pour comprendre sa logique consiste à poser une corde le plus précisément possible sur l'arc que l'on désire mesurer. Pour pouvoir aisément calculer la longueur de la corde, on lui impose de suivre un trajet polygonal. On punaise les sommets de la corde sur l'arc étudié, de telle manière à ce que les punaises se succèdent, comme sur la figure de droite. En ajoutant de plus en plus de punaises, on impose à la corde de suivre de plus en plus précisément l'arc. Une fois accrochée une infinité de punaises régulièrement espacées on obtient la longueur recherchée. Si cette approche possède l'avantage d'être pertinente, même dans le cas d'un arc non dérivable, donner un sens rigoureux à l'idée d'une infinité de punaises régulièrement espacées serait un peu délicat. Jordan propose plutôt la borne supérieure des longueurs des différentes cordes imaginables, attachées avec un nombre fini de punaises. Cette démarche allie la rigueur avec une généralisation de la longueur aux arcs non nécessairement dérivables.
Par delà le fait de pouvoir traiter des courbes non dérivables, de nouvelles méthodes deviennent utilisables qui ne l'étaient pas avec la définition précédente. Un exemple est donné avec le théorème isopérimétrique. Ce théorème stipule que toute surface possède une aire plus petite que celle du disque de même périmètre. Certaines démonstrations, présentées dans l'article sur cette question, nécessitent la définition de longueur au sens de Jordan.
Approche formelle
L'ensemble d'arrivée n'est maintenant plus nécessairement euclidien, (E, d) désigne dans ce paragraphe un espace métrique et I toujours un intervalle de ℝ. Le couple (I, f) est un arc, c'est-à-dire une fonction continue de I dans E. La logique suivie pour la définition est proche de celle utilisée pour l'intégrale de Riemann. Soit S une suite finie a0, … , an strictement croissante d'éléments de I. Une telle suite est appelée une subdivision de l'intervalle [a0, an] de I.
À la suite S on peut associer la longueur L(S), définie par :

La valeur L(S) est appelée ici longueur de la ligne polygonale de sommets les images de la suite S par f. L'inégalité triangulaire impose de définir la longueur de l'arc C comme supérieure à celle d'une ligne polygonale associée à une subdivision d'un intervalle de I. La ligne droite que suit la ligne polygonale entre deux sommets consécutifs est en effet le chemin le plus rapide entre ces deux points et passer par la courbe C est nécessairement plus long. En revanche, si la subdivision est très fine, on peut espérer obtenir une bonne approximation de la longueur de C, ce qui justifie la définition suivante :
- La longueur de l'arc C est la variation totale de f, c'est-à-dire la borne supérieure de l'ensemble des longueurs des lignes polygonales de sommets les images d'une subdivision d'un intervalle de I[27].
Une telle définition n'impose pas à la longueur d'être finie. Par exemple une droite est de longueur infinie. Des contre-exemples moins triviaux sont donnés par la figure de droite ou encore la courbe de Peano, qui est continue mais nulle part dérivable, et dont l'image du segment [0,1] est l'ensemble des points d'un carré de côté 1. Ceci donne lieu à la définition suivante :
- Un arc est dit rectifiable si sa longueur est finie.
Propriétés
- La longueur d'un arc géométrique est supérieure à la distance qui sépare les extrémités, si elles existent.
Cette proposition n'est que la généralisation de l'inégalité triangulaire. Dans un espace euclidien, la trajectoire la plus courte entre deux points est le segment de droite. Tout support d'arc géométrique d'extrémités ces deux points est nécessairement plus long. Cette proposition n'a d'intérêt que si les deux extrémités ne sont pas confondues, comme pour le cercle. - La longueur de deux supports géométriques d'arcs qui partagent une extrémité est la somme des longueurs des deux supports.
Cette proposition est encore très intuitive. Suivre une route qui va de A à B, puis continuer jusqu'à un point C représente la même longueur que suivre la même route pour aller de A à C. - Si l'ensemble d'arrivée est un espace affine, muni d'une distance issue d'une norme, alors une homothétie d'un rapport k, appliquée à un arc géométrique, accroit la longueur de l'arc d'un rapport k.
Une dernière propriété est utile pour assurer la cohérence de la définition de longueur. Ici E désigne à nouveau un espace euclidien :
- Soit (I, f) un arc paramétré de classe C1 rectifiable. L'intégrale de la norme de la dérivée de f sur l'intervalle I est convergente et la longueur L de l'arc (I, f) au sens de Jordan est égale à celle définie par l'intégrale de la norme de sa dérivée.
- L'intégrale de la norme de la dérivée de f sur l'intervalle I est convergente et la longueur L de l'arc (I, f) au sens de Jordan est égale à celle définie par l'intégrale de la norme de sa dérivée[28] :
Soit ε un réel strictement positif. Le fait que l'arc soit rectifiable se traduit par l'existence d'un découpage de I : a0, …, an tel que la longueur de la ligne polygonale des images par f approxime L, la longueur de l'arc à ε/3 près. Ces hypothèses se traduisent par la majoration :
Sur le segment [a0, an], la dérivée de f est une fonction uniformément continue. On en déduit que, quitte à affiner le découpage choisi :
Ceci montre que, d'après l'inégalité des accroissements finis pour les fonctions à valeurs vectorielles :
En sommant ces n – 1 majorations, on obtient :
En combinant les majorations (1) et (2), on obtient :
La dernière majoration est vraie pour tout découpage de I suffisamment fin. Ce qui indique que l'intégrale impropre de la norme de la dérivée de f entre a et b est convergente. Autrement dit, quitte à encore affiner le découpage, on dispose aussi de la troisième majoration :
En sommant les trois majorations (1), (2) et (3), on obtient :
La dernière majoration étant vraie pour tout ε strictement positif, l'égalité entre la longueur de l'arc et l'intégrale est bien vérifiée.


Les fonctions bornées de I dans E sont dotées de la distance de la continuité uniforme. Il est naturel de s'interroger sur la continuité de la fonction qui, à un arc, associe sa longueur. La figure de gauche montre que cette fonction n'est pas continue. En effet, dire qu'un arc, en rouge sur la figure, est proche d'un autre, le cercle bleu sur la figure, signifie que l'arc se trouve dans une espèce de tube, de petite largeur. La courbe en rouge montre qu'il est possible de construire une telle courbe qui oscille suffisamment pour avoir une longueur très différente. En revanche, si la courbe rouge est proche de la bleue, sa longueur ne peut être beaucoup plus petite que la bleue. Celle de plus petite longueur est illustrée à droite en vert. On parle de semi-continuité inférieure.
- La fonction « longueur » (i.e. variation totale), à valeurs dans [0, +∞], est semi-continue inférieurement sur l'espace (muni de la distance de la convergence uniforme) des fonctions bornées de I dans un espace métrique E.
En effet[29], pour toute subdivision σ d'un intervalle de I, la fonction f ↦ V(f, σ) est continue, donc la fonction longueur est semi-continue inférieurement, comme borne supérieure des V(f, σ).
Contenu de Minkowski
Motivation

Minkowski s'intéresse surtout aux courbes fermées et simples car elles définissent une frontière d'un espace compact dans le plan euclidien. Les résultats qu'il établit sont particulièrement intéressants s'il peut les généraliser aux dimensions supérieures.
Les outils issus de la géométrie différentielle ne sont pas toujours très adaptés pour cela. Un exemple est donné par le théorème isopérimétrique, dans le cas général on cherche à démontrer qu'un solide d'un espace euclidien de dimension n possède un volume plus petit que celui de la boule de même surface. Le terme de boule de rayon r désigne l'ensemble des points à une distance inférieure à r d'un point donné appelé centre. Il n'est pas trop complexe de montrer que la courbure moyenne en chaque point d'une surface, frontière d'un solide qui atteint l'optimum isopérimétrique, est nécessairement constante. En dimension 2, il est très simple de montrer que l'unique courbe simple et fermée de courbure moyenne constante est le cercle, une démonstration naturelle est l'œuvre de Hurwitz et utilise l'inégalité de Wirtinger[30]. En dimension 3, la démonstration est connue, mais elle est suffisamment technique[31] pour ne dater que du début du XXe siècle. Le cas général n'est toujours pas démontré[32].

La définition de Jordan pour la longueur d'une courbe n'est pas adaptée non plus car elle ne se généralise pas directement aux dimensions supérieures. La généralisation naturelle consisterait à définir l'aire de la surface d'une portion de cylindre comme la borne supérieure de la surface d'un polyèdre dont les sommets se trouveraient sur la frontière du cylindre. L'exemple sur la droite illustre l'inconsistance d'une telle généralisation. Le polyèdre utilisé est un lampion dont les sommets sont situés sur des hexagones parallèles, chaque fois décalés d'un douzième de tour. Si les plans des hexagones se rapprochent de plus en plus, la surface du polyèdre augmente jusqu'à l'infini[33].
Minkowski trouve une solution pour définir la longueur d'un arc qui résiste au passage à une dimension supérieure. Son approche intuitive est différente de celles considérées jusqu'ici. Il ne s'appuie pas comme Jordan sur la longueur d'une ligne polygonale, mais directement sur la fonction volume de l'espace euclidien de dimension n. Cette fonction est en général définie par la mesure de Lebesgue. Pour une valeur ε, suffisamment petite, il considère les points à une distance inférieure à ε de la courbe C qu'il étudie. Il obtient un ensemble, illustré en rose sur un exemple en dimension 2 sur la figure de gauche, la courbe C est représentée en bleu. Un tel ensemble est appelé un tube.
Si la valeur ε diminue, le volume du tube se rapproche du produit de la longueur de l'arc par le volume de la boule de dimension n – 1 et de rayon ε. Dans le cas du cercle de rayon r et en dimension 2, le tube est constitué de la zone de l'espace compris entre un cercle de rayon r + ε et un autre de même centre et de rayon r – ε. Son volume est exactement 2πr que multiplie 2ε. En dimension 3, le tube est un tore, une fois encore son volume est exactement le produit de 2πr par la surface d'un disque de rayon ε. Cette définition, si elle est un peu plus complexe à mettre en œuvre, se généralise aisément aux dimensions supérieures.
Si ε est un entier plus petit que r, la zone Cε est celle qui se trouve à l'intérieur d'un disque de rayon r + ε et à l'extérieur du disque ouvert de rayon r – ε. La surface Vol (Cε) est égale à :
Or, 2πr correspond à la longueur du cercle et en dimension 1, la boule de rayon ε est de volume égal à 2ε en dimension 1. Le contenu de Minkowski est bien égal à la longueur du cercle.
Formalisme
Minkowski et Hausdorff développent des outils permettant de mieux appréhender l'étude générale des solides. L'ensemble étudié est celui des compacts non vides d'un espace euclidien E, de dimension n. La somme de Minkowski associe à deux ensembles A et B le solide A + B composé des sommes d'éléments de A et de B. Cet ensemble est équipé d'une distance, dite distance de Hausdorff. Le tube étudié correspond à la somme d'un compact C, correspondant à la courbe dont on souhaite mesurer la longueur et de la boule de rayon ε, il est noté ici Cε.
Si la courbe C est simple et fermée et de classe C2, alors le volume du tube Vol(Cε) s'exprime en fonction de la longueur LC de l'arc C et du volume Vol(Bn-1(ε)) de la boule d'un espace euclidien de dimension n – 1 et de rayon ε, ceci à condition que ε reste suffisamment petit :
Si la courbe n'est pas fermée, l'égalité reste vraie si l'on ajoute le volume d'une boule de rayon ε en dimension n. En effet, deux demi-boules vont s'ajouter, chacune à l'une des extrémités de la courbe, on obtient :
Quelle que soit la configuration précédente, on obtient une nouvelle manière de définir la longueur d'un arc[34] :
- Le contenu 1-dimensionnel d'un ensemble C d'un espace euclidien de dimension n, noté M1(C), est la limite suivante, quand elle existe :
Cette définition est bien une généralisation de la longueur définie précédemment :
- Si C est l'ensemble d'arrivée d'un arc paramétré compact de classe C2, la longueur de C est égale à son contenu 1-dimensionnel.
Cette définition est particulièrement pertinente dans le cas de l'étude de la longueur de la frontière d'une surface S compacte en dimension 2 de frontière C. Si la frontière est paramétrable par un arc de classe C2, on dispose du théorème suivant, appelé formule de Steiner-Minkowski :
- La longueur LC de l'arc C est égale à la limite suivante :
Le contenu de Minkowski permet de généraliser à de nombreuses surfaces cette formule.
Fixons les notations, E est un espace euclidien de dimension n, ([a, b], f) est un paramétrage curviligne de classe C2 d'un arc géométrique, fermé et simple et dont l'image est égale à C. Dire que le paramétrage est fermé revient à dire que f(a) est égal à f(b), dire qu'il est simple est équivalent à dire que si s et t sont deux éléments de ]a, b[, alors f(s) est différent de f(t). Enfin, dire que le paramétrage est curviligne revient à dire que la norme de la dérivée de f(t) est toujours égale à 1, si t est un élément de [a, b]. La valeur ε désigne un réel strictement positif, compris entre 0 et μ, où μ est un réel strictement positif à déterminer. Ht désigne l'hyperplan de E orthogonal à f(t) et Ba,μ la boule unité fermée de l'hyperplan Ha et de rayon μ. On note ut la dérivée de f au point t et vt le vecteur de norme 1 colinéaire à la dérivée seconde de f et de même sens. Dire que f est un paramétrage curviligne implique que ut et vt sont orthogonaux. Enfin, on note c(t) la courbure de f en t, la dérivée seconde de f en t est égale au produit de c(t) par vt.
La technique utilisée pour la démonstration consiste à construire un plongement ψ de [a, b]xBa,μ dans Cμ de classe C1. Ce plongement fournit le bon changement de variable pour calculer l'intégrale donnant l'aire de Cε. Pour construire ψ, on construit une application φt de classe C1 de [a, b] à valeurs dans les rotations de E, telle que l'image de ua par φt soit égale à ut.
- Construction de φt :
- Equation différentielle :
- Une solution élégante consiste à construire φt comme la solution d'une équation différentielle linéaire. Pour cela, on définit une application χ d'un ensemble D dans L(E) l'ensemble des endomorphismes de l'espace E. Ici D désigne les couples (u, v) de vecteurs de E tels que u et v soient de normes égales à 1 et tels que u et v soient orthogonaux. L'endomorphisme χ(u,v) associe à u le vecteur v, à v le vecteur -u et le vecteur nul à tout vecteur orthogonal à u et à v. On remarque que pour tout vecteur z de E, le produit scalaire de z avec son image par χ(u,v) est nul. En effet, il est possible d'écrire z sous la forme α.u + β.v + w, où α et β sont deux scalaires et w un vecteur orthogonal à u et à v. On a bien, si <.,.> désigne le produit scalaire :
- Cette application nous permet de définir la fonction ψ, de [a, b] dans L(E), par :
- L'application ψ est bien continue, elle est en effet composée d'applications continues. Il existe une petite difficulté si la courbure c(t) est nulle, car vt n'est pas défini, mais définir ψ comme nulle en ces points est clairement un prolongement par continuité, la norme de ψt étant égale à c(t). La norme choisie ici pour L(E) est celle qui, à un endomorphisme associe la borne supérieure de la norme de l'image de la boule unité. On considère l'équation différentielle suivante, sur [a, b] et à valeurs dans L(E):
- La continuité de ψ et la compacité de [a, b] montrent que la fonction, qui à t associe la norme de ψ, atteint sa borne supérieure m. L'application qui à X associe la composée de ψ et de X est donc continue et m-lipschitzienne. Le théorème de Cauchy-Lipschitz garantit l'existence d'une solution unique φ à l'équation différentielle. Il est même possible de donner une expression explicite de φ :

À l'exception du caractère un peu inhabituel des ensembles utilisés ici, la méthode proposée n'utilise qu'une équation différentielle linéaire très simple. L'application φ permet presque de définir un repère de Frenet. Il suffirait d'associer au point a une base de Frenet et la base de Frenet serait, au point t son image par φ. Ce résultat n'est vrai que si la courbe est birégulière, c'est-à-dire que la dérivée seconde de f ne s'annule jamais. Après le premier point d'inflexion, il n'existe aucune raison de penser que l'image de v0 soit encore colinéaire à la dérivée seconde de f. Il suffit maintenant de vérifier que φ est bien l'application recherchée.
- L'application φ est à valeurs dans un ensemble de rotations et l'image de ua par φt est égale à ut :
- Montrons tout d'abord que φ est à valeurs dans un ensemble de rotations. ce qui revient à montrer que si z est un vecteur de E, φt(z) est de même norme que z. Ce résultat est trivialement vrai si t est égal à a car φa est l'identité. Il suffit de montrer que la dérivée de la fonction, qui à t associe le carré de la norme de φt(z), est nulle, pour établir que φt est une isométrie :
- Il reste à montrer que le déterminant de φt est égal à 1. Comme φt est une isométrie, son déterminant est égal à ±1. L'image de l'application qui à t associe det φt est un connexe car l'application est continue. Comme en a, l'application vaut 1, elle vaut 1 partout et le déterminant de φt est bien égal à 1.
- Montrons ensuite que φt(ua) est bien égal à ut. Pour cela, il suffit de vérifier que les deux arcs, qui à t associe φt(ua) d'une part et ut d'autre part ont même valeur initiale et satisfont à la même équation différentielle linéaire. L'unicité de la solution, garantie par le théorème de Cauchy-Lipschitz, montre l'égalité. Par construction φa est égal à l'identité ; les deux arcs ont donc bien même valeur initiale. Vérifions maintenant que les deux arcs sont solutions de la même équation différentielle :
- D'autre part :
On en déduit que φt(Ha) est bien égal à Ht. En effet, Ha est l'orthogonal de ua, son image par φt est l'orthogonal de φt(ua) car φt est une rotation. Il suffit de remarquer que φt(ua) est égal à ut pour conclure.
- Injectivité de Γ :

Pour que l'application Γ soit un plongement, il est nécessaire de bien choisir la valeur μ. Si elle est trop élevée, l'application Γ n'est pas nécessairement injective. Un exemple est donné sur la figure de droite. Le plus petit rayon de courbure est donné par le point de cercle osculateur violet. La valeur μ est choisie plus grande que le rayon du cercle osculateur, appelé rayon de courbure. Le point rouge est élément de l'hyperplan orthogonal à la tangente du point de cercle osculateur violet, et il est à une distance égale à cette valeur de μ. Les points à une distance inférieure ou égale à μ de la courbe sont illustrés en vert. Le point rouge est aussi élément du plan orthogonal d'un autre point, illustré en jaune. Si μ est choisi plus petit que le plus petit rayon de courbure atteint par les points de la courbe, cette situation ne peut pas se produire. L'application Γ est alors localement injective.
- Injectivité locale de Γ :
- La fonction c(t) qui à t associe la courbure de l'arc au point f(t) est continue. Elle est définie sur un compact, elle atteint sa borne supérieure. Notons rm l'inverse de cette borne, qui correspond au plus petit rayon de courbure de l'arc. On suppose que μ est choisi plus petit que rm/2. L'objectif est de montrer que Γ est localement injective, c'est-à-dire que si t est un élément de [a, b], Γ est injective sur l'ensemble ]t-δ, t+δ[xBa,μ. La valeur δ correspond à un nombre réel strictement positif indépendant de t et à déterminer.
- Pour simplifier les notations, on suppose, quitte à translater l'intervalle [a, b], que t est égal à 0. On suppose de plus, quitte à modifier le repère, que f(0) est égal au vecteur nul. On va montrer qu'un point p image par Γ d'un point (0, p) de ]t-δ, t+δ[xBa,μ n'a pas d'autre antécédent dans cet ensemble. Dire que p est une telle image, revient à dire que sa norme est plus petite que μ, donc que rm/2 et que p est orthogonal à u0. On considère un autre antécédent de première coordonnée notée t et l'on va montrer que t est nécessairement plus grand qu'une valeur δ. Dire que t est un autre antécédent implique que p est dans le plan orthogonal à ut et passant par f(t). Ce qui montre l'égalité :
- La formule de Taylor-Lagrange montre l'existence d'une valeur τ1, comprise entre 0 et t, telle que :
- Le même raisonnement montre l'existence de deux valeurs τ2 et τ3, aussi comprises entre 0 et t, telles que :
Si l'on choisit δ plus petit que min(1, 1/cm)/6, on est assuré que le terme <p, ut> est strictement plus petit que le deuxième produit scalaire, et l'injectivité locale sur l'intervalle ]t-δ, t+δ[xBa,μ est bien garantie.
- Injectivité globale de Γ :


L'injectivité locale n'implique pas l'injectivité de Γ. L'illustration de droite montre la raison. Si la courbe est suffisamment pincée, un point d'abscisse éloignée peut être arbitrairement proche du point étudié. Il faut alors vérifier qu'une zone rouge, à l'image de la figure, n'existe pas si μ est bien choisi. Comme par hypothèse, l'arc ne contient pas de point double, la configuration désagréable serait celle de gauche, avec une infinité de brins de l'arc qui s'approchent de plus en plus du point critique. La compacité du segment [a, b], impliquant celle du graphe C empêche l'apparition de ce phénomène.
- Pour s'en persuader, considérons la fonction qui à t associe le minimum de la distance entre f(t) et l'image par f des intervalles [a, t - δ] et [t + δ, b]. Comme la fonction distance est continue et que l'union des segments [a, t - δ] et [t + δ, b] est un compact, ce minimum est atteint. Comme l'arc est simple, c'est-à-dire qu'il n'admet pas de point multiple, ce minimum est différent de 0. La fonction de [a, b] dans ℝ qui à t associe le minimum défini précédemment est encore continue. Elle est encore définie sur un compact, ce qui implique qu'elle atteint encore son minimum μ1 qui n'est pas nul.
- Si la valeur μ est choisie strictement plus petite que μ1/2 (il faut diviser par 2 car la contrainte n'est pas que la zone verte ne doit pas rencontrer de manière indue la courbe C en bleu, mais que la zone verte ne s'intersecte pas avec elle-même) et que rm/2, les preuves précédentes garantissent l'injectivité de Γ.
Pour pouvoir effectuer le changement de variable dans le calcul du volume, il faut encore s'assurer que l'ensemble d'arrivée de Γ restreint à [a, b]xBa,ε, où ε est un nombre réel strictement positif et plus petit que μ est bien Cε. Elle est plus facile à vérifier.
- Surjectivité de Γ restreint à [a, b]xBa,ε dans Cε:
- Soit p un point de Cε. La fonction de C dans ℝ, qui à un point associe sa distance à p, est continue. Elle atteint son minimum en un point f(t), avec une distance inférieure à ε par hypothèse. Si h est un réel tel que t + h soit un élément de [a, b] la distance entre p et f(t+h) est plus grande que le minimum précédemment cité. On en déduit :
- La majoration est vraie pour les valeurs positives comme négatives de h, ce qui montre que p - f(t) est orthogonal à ut. Une autre manière de dire les choses est que p est dans l'image de Γ. Plus précisément, son antécédent est (t, φt-1(p- f(t))).
- Calcul du jacobien :
- Pour effectuer le changement de variable, il est utile de calculer le déterminant jacobien de ψ en un point (t, z). Pour cela calculons dans un premier temps la différentielle de ψ en ce point. Soit vt,a l'antécédent du vecteur normalisé de u't par φt, si la dérivée seconde de f n'est pas nulle et un vecteur de Ha de norme 1 et orthogonal à ua si la dérivée seconde est nulle. On note Kt,a l'hyperplan de Ha orthogonal à vt,a. On note (td, zd) un petit vecteur de Ba,μ tel que la somme du point (t, z) et de (td, zd) soit dans Ba,μ. Enfin, on utilise les notations :
- On a :
- On en déduit la différentielle :
- Pour le calcul du déterminant, on remarque que la différentielle possède deux espaces stables, celui engendré par ut et vt, puis Kt,a. Sur l'espace Kt,a, la différentielle est une rotation ; son déterminant est égal à 1 ; le jacobien recherché est celui de l'espace vectoriel de dimension 2 engendré par les deux vecteurs ut et vt. Dans cette base, la matrice M est égale à :
Le résultat n'est pas étonnant. Il signifie que si la courbure est localement nulle, l'application ψ ne modifie pas le volume. Le même phénomène se produit aux alentours de la courbe C. En revanche, si un petit volume est choisi avec une coordonnée positive, c'est-à-dire dans la concavité de la courbure, alors le volume diminue. Il irait jusqu'à 0 si l'on se rapprochait du rayon de courbure, égal à 1/c(t), ce qui ne peut se produire avec le choix de μ, qui ne dépasse jamais la moitié du rayon de courbure. En revanche, dans la direction opposée, le volume augmente.
- Calcul du volume de Cε :
- On peut maintenant appliquer le changement de variable ψ :
- Or le solide [a, b]x Ba,μ est symétrique par rapport à Ka et le volume de la surface coupée à l'ordonnée ζ est exactement le même que celle coupée à l'ordonnée -ζ. La deuxième intégrale est égale à 0. On trouve :
Le contenu 1-dimensionnel de la courbe C est égal à b – a, c'est-à-dire à la longueur de la courbe, car son paramétrage correspond à une abscisse curviligne. Dans le cas du cercle et en dimension 3, on retrouve une formule connue, le volume d'un tore. Dans le cas d'une courbe qui n'est pas fermée, la démonstration est exactement la même, il suffit d'ajouter les deux demi-boules aux extrémités.
Dans le cas d'une courbe de classe C2 et admettant des points doubles, montrer que le contenu 1-dimensionnel de Minkowski est encore égal à la longueur n'est pas très compliqué, mais l'égalité du produit précédent et du volume du tube n'est plus vérifiée. Le résultat est encore vrai pour les courbes de classe C1, les polygones ou les courbes fermées non vides compacts et convexes en dimension 2, mais les démonstrations sont différentes.
Courbe fractale


Dès 1872, Karl Weierstrass montre qu'une courbe peut avoir un comportement étrange ; il construit un exemple d'arc, par définition continu, et nulle part différentiable. Plus tard, Peano construit sa courbe, dont l'image est l'ensemble des points d'un carré de côté 1. En 1904, le mathématicien suédois von Koch trouve un exemple concret de courbe répondant au cahier des charges de Weierstrass, à travers un étrange flocon[36]. Tous ces exemples correspondent à ce qui est maintenant appelé une fractale.
Cette famille de courbes, initialement considérées comme un peu pathologiques, s'avère essentielle pour une meilleure compréhension de certaines branches des mathématiques. L'étude d'un système dynamique comme celui de Lorenz porte sur une équation différentielle dont le comportement limite se situe à l'intérieur d'une zone géométrique définie par une telle courbe (pour être plus précis, la zone correspond à l'adhérence d'une telle courbe)[37].
Pour l'analyse de telles courbes, un équivalent de la longueur s'avère nécessaire. Or pour la courbe de Peano, la définition différentielle n'a pas de sens et celle de Jordan donne l'infini. Si le contenu 1-dimensionnel de Minkowski donne aussi l'infini, il n'est pas très compliqué de l'adapter pour trouver une réponse qui a du sens. Si P désigne l'ensemble d'arrivée de la courbe de Peano :
Ici, Pε désigne l'ensemble des points à distance inférieure à ε de P. L'astuce a consisté à diviser le rapport, non pas par le volume d'une boule (n – 1)-dimensionnelle, mais (n - 2)-dimensionnelle. Pour une nappe de classe C2 et de dimension 2, le contenu correspond à la mesure de la surface. Pour l'attracteur de Lorenz ou le flocon de Koch, aucun entier k ne permet de définir un contenu (n – k)-dimensionnel qui ne soit ni 0 ni l'infini. En revanche, il est possible d'utiliser une définition du volume d'une boule de dimension qui ait du sens, même si ζ n'est pas un entier :
Ici Γ désigne la fonction gamma. Le contenu de Minkowski se généralise ainsi à des dimensions non entières. Cette dimension, qui permet de donner un sens à la longueur d'un arc, est appelée dimension de Hausdorff.
Notes et références
- ↑ Tablettes de Suse - voir par exemple π et √2 chez les babyloniens.
- ↑ Archimède, De la sphère et du cylindre - De la mesure du cercle - Sur les conoïdes et les sphéroïdes, tome 1 Belles Lettres (2003) (ISBN 2251000240).
- ↑ Karine Chemla et Guo Shuchun, Les neuf chapitres : Le classique mathématique de la Chine ancienne et ses commentaires [détail de l’édition], p. 144-147.
- ↑ Torricelli, Opere, III, p. 368 et 477 : Lettres à Ricci de 1646 et à Cavalieri (1598-1647).
- ↑ (en) James W. P. Campbell, « Scientific Work of Christopher Wren », .
- ↑ Voir par exemple R. Ferreol et J. Madonnet, « Parabole semi-cubique », sur Encyclopédie des formes mathématiques remarquables, .
- ↑ (la) J. Wallis, Tractatus duo, Opera t. 1 (1659), p. 551.
- ↑ Ces preuves sont publiées par van Schooten en 1659 dans la Géométrie de Descartes.
- ↑ (la) P. de Fermat, Dissertatio de linearum curvarum cum lineis rectis comparatione, Œuvres t.1 (1660), p. 211.
- ↑ Marcel Berger et Bernard Gostiaux, Géométrie différentielle : variétés, courbes et surfaces [détail des éditions], p. 302.
- ↑ a et b Berger et Gostiaux, p. 303.
- ↑ « Il est essentiel de remarquer que la […] longueur L [d'un arc ([a, b], f)] n'est jamais égale à la longueur du graphe de f ; celle-ci est un élément de l'intervalle ]L, L + b – a]. » — Gustave Choquet, Cours d'analyse, vol. II : Topologie, p. 104.
- ↑ Gottfried Wilhelm Leibniz, La naissance du calcul différentiel, rééd. Vrin, 2000 (ISBN 2711609979), p. 203.
- ↑ « Lettre de Fermat à C. de la Chambre du Dimanche 1er janvier 1662 », dans Paul Tannery et Charles Henry, Œuvres de Fermat (lire en ligne), p. 458.
- ↑ Pour plus de détails, voir par exemple : J.-P. Pérez et E. Anterrieu, Optique : Fondements et applications, Dunod (7e édition) 2004 (ISBN 978-210048497-3).
- ↑ Galilée avait imaginé que la solution au problème brachistrochrone était le cercle : Galileo Galilei Discorsi e dimostrazioni matematiche, intorno à due nuove scienze Édité par Appresso gli elsevirii (1638)
- ↑ (en) John J. O'Connor et Edmund F. Robertson, « The brachistochrone problem », sur MacTutor, université de St Andrews.
- ↑ P. Maupertuis, Accord de différentes lois de la nature, texte original de 1744 édité dans Œuvres de Maupertuis, vol. IV, 1768, p. 16-17.
- ↑ B. Riemann Sur les hypothèses sous-jacentes à la géométrie (Über die Hypothesen welche der Geometrie zu Grunde liegen) publié par Dedekind dans Abhandlungen der Königlichen Gesellschaft der Wissenschaften zu Göttingen vol. 13, 1867 et accessible en anglais lire
- ↑ Pour plus de détails sur les variétés riemanniennes, voir (en) Marcel Berger, A Panoramic View of Riemannian Geometry, [détail de l’édition].
- ↑ J. Peiffer, Euler: Variations autour d'une courbe, Les cahiers de science et vie, no 68, 2002, p. 72-79
- ↑ F. Martin-Robine, Histoire du principe de moindre action, Vuibert, 2006 (ISBN 978-2711771516)
- ↑ Dans un livre de géométrie différentielle, la définition précédente est en effet parfaitement suffisante : Berger et Gostiaux, p. 315.
- ↑ G. Peano, Sur une courbe, qui remplit toute une aire plane, dans Mathematische Annalen, vol. 36, 1890, p. 157-160
- ↑ (de) H. Minkowski, Geometrie der Zahlen, Teubner, Leipzig, 1896 ; republié par Johnson, New York, 1968
- ↑ C. Jordan, Cours d'analyse de l'école polytechnique, 3 volumes, Jacques Gabay, première publication entre 1882 et 1887 (1991) (ISBN 978-287647018-7)
- ↑ Cette définition est équivalente à celle de Berger et Gostiaux, p. 314.
- ↑ La démonstration présentée ici est un grand classique ; on la trouve par exemple dans Jacques Dixmier, Cours de mathématiques du premier cycle Gauthier-Villars, 1976 (ISBN 978-2-04-002687-5), chap. 53.
- ↑ Choquet, p. 138.
- ↑ (en) A. P. Burton et P. Smith, « Isoperimetric inequalities and areas of projections in Rn », dans Acta Mathematica Hungarica, vol. 62, no 3-4, 1993
- ↑ (de) H. Liebmann, « Über die Verbiegung der geschlossenen Flachen positiver Krümm », dans Math. Ann., vol. 53, 1900, p. 81-112
- ↑ (en) Robert Osserman, « The isoperimetric inequality », Bull. Amer. Math. Soc., vol. 84, no 6, , p. 1183-1238 (lire en ligne) : p. 1188.
- ↑ Cet exemple est tiré de Berger et Gostiaux, p. 226.
- ↑ On trouve cette définition dans Osserman 1978, p. 1189.
- ↑ La démonstration présentée ici s'inspire de celle du corollaire de Berger et Gostiaux, p. 254.
- ↑ H. von Koch, « Une méthode géométrique élémentaire pour l'étude de certaines questions de la théorie des courbes planes », Acta Math., no 30, 1906, p. 145-174.
- ↑ (en) Edward N. Lorenz, « Deterministic Nonperiodic Flow », J. Atmos. Sci., vol. 20, , p. 130-141 (DOI 10.1175/1520-0469(1963)020<0130:DNF>2.0.CO;2, lire en ligne).
Liens externes
- Distance à vol d'oiseau entre deux points de la surface terrestre
- Périmètre de la représentation graphique d'une fonction f(x) (à ne pas confondre avec la longueur de l'arc f)
v · m  Courbe - Éléments de navigation Courbe - Éléments de navigation | |
|---|---|
| Modes de génération | |
| Éléments remarquables | |
| Traçage |
|
| Transformées | |
| |
 Portail de la géométrie
Portail de la géométrie
























![{\displaystyle [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/738f7d23bb2d9642bab520020873cccbef49768d)





![{\displaystyle L_{0}=\int _{0}^{x_{0}}\operatorname {cosh} \left({\frac {x}{a}}\right)\mathrm {d} x=\left[a\operatorname {sinh} \left({\frac {x}{a}}\right)\right]_{0}^{x_{0}}=a\operatorname {sinh} \left({\frac {x_{0}}{a}}\right).}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a49ff0a2bfecb3211f1070fc1f887c5dc2af772b)



![{\displaystyle L_{0}=\int _{0}^{x_{0}}{\sqrt {1+{\frac {9a^{2}}{4}}x}}\;\mathrm {d} x={\frac {4}{9a^{2}}}\int _{0}^{{\frac {9a^{2}}{4}}x_{0}}{\sqrt {1+u}}\;\mathrm {d} u={\frac {8}{27a^{2}}}\left[(1+u)^{\frac {3}{2}}\right]_{0}^{{\frac {9a^{2}}{4}}x_{0}}={\frac {(4+9a^{2}x_{0})^{\frac {3}{2}}-8}{27a^{2}}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/955519469cf2846ecdd85c70dc97fb62a7d1feb6)














![{\displaystyle \forall i\in [1,n],\;\forall x\in [a_{i-1},a_{i}]\quad \left\|{\frac {\mathrm {d} f}{\mathrm {d} x}}(a_{i-1})-{\frac {\mathrm {d} f}{\mathrm {d} x}}(x)\right\|\ \leq {\frac {\epsilon }{3(a_{n}-a_{0})}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6e0bb055fec974189ec69cdf68799ab610464fdb)
![{\displaystyle \forall i\in [1,n-1]\quad \|f(a_{i})-f(a_{i-1})-{\frac {\mathrm {d} f}{\mathrm {d} x}}(a_{i-1})(a_{i}-a_{i-1})\|\leq {\frac {\epsilon (a_{i}-a_{i-1})}{3(a_{n}-a_{0})}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/083b4e1c4588250e823a8de25c0f1c80d91a289d)










![{\displaystyle \forall t\in [a,b]\quad \psi _{t}=c(t)\chi _{(u_{t},v_{t})}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1f324f9e830485158edf38fe437fb705407f5635)

![{\displaystyle \forall t\in [a,b]\quad \varphi _{t}=\exp \left(\int _{a}^{t}\psi _{\tau }\mathrm {d} \tau \right)\quad {\text{avec, si}}\quad m\in {\mathcal {L}}(E)\quad \exp(m)=\sum _{n=0}^{\infty }{\frac {m^{n}}{n!}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/20e214126a37b84f6199238e2f6f3b40a49665c9)

![{\displaystyle \forall t\in [a,b]\quad {\frac {\mathrm {d} \varphi _{t}(u_{0})}{\mathrm {d} t}}={\frac {\mathrm {d} \varphi _{t}}{\mathrm {d} t}}(u_{0})=\psi _{t}\circ \varphi _{t}(u_{0})\quad {\text{donc}}\quad {\frac {\mathrm {d} \varphi _{t}(u_{0})}{\mathrm {d} t}}=\psi _{t}\left(\varphi _{t}(u_{0})\right).}](https://wikimedia.org/api/rest_v1/media/math/render/svg/861a2071ee62b77e4794c2a9cabe5ab1076a7b11)
![{\displaystyle \forall t\in [a,b]\quad {\frac {\mathrm {d} u_{t}}{\mathrm {d} t}}=c(t)v_{t}=c(t)\chi _{(u_{t},v_{t})}=\psi _{t}(u_{t})\quad {\text{donc}}\quad {\frac {\mathrm {d} u_{t}}{\mathrm {d} t}}=\psi _{t}(u_{t}).}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e23b51ab9f5de4b0c32f62ef3edfb20c85428736)









![{\displaystyle Vol(C_{\epsilon })=\int _{C_{\epsilon }}1\mathrm {d} \sigma =\int _{[a,b]\times B_{\mu ,a}}|\det D\varphi _{t,z}|\;\mathrm {d} t\mathrm {d} \zeta \mathrm {d} z_{k}=(b-a)Vol(B_{n-1}(\epsilon ))-\int _{[a,b]\times B_{\mu ,a}}c(t)\zeta \;\mathrm {d} t\mathrm {d} \zeta \mathrm {d} z_{k}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3f66fc83724a14b03d26d5f9fefb46974485fd7b)













