Çevre açı

Geometride, çevre açı, çember üzerinde iki sekant (kesen) çizgisi kesiştiğinde bir çember üzerinde oluşan açıdır. Çember üzerindeki bir nokta (açının tepe noktası) ile çember üzerinde verilen diğer iki noktanın oluşturduğu açı olarak da tanımlanabilir.

Eşdeğer olarak, bir çevre açı, bir bitiş noktasını paylaşan çemberin iki kirişiyle tanımlanır.

Çevre açı teoremi, bir çevre açının ölçüsünü, aynı yayı oluşturan merkezi açının ölçüsü ile ilişkilendirir.

Çevre açı teoremi, Öklid'in "Elementler" kitabının 3. kitabında Önerme 20 olarak görünür.

Teorem

Açıklama

Çevre açı teoremi, bir çember içine çizilmiş bir ${\displaystyle \theta }$ açısının, çember üzerindeki aynı yaya karşılık gelen (veya aynı yayı gören) merkezi açı ${\displaystyle 2\theta }$'nın yarısı olduğunu belirtir. Bu nedenle, tepesi çember üzerinde farklı konumlara taşındığında açı değişmez.

İspat

Bir kirişin çap olduğu çevre açılar

Şekilde görüldüğü gibi ${\displaystyle O}$ bir çemberin merkezi olsun. Çember üzerinde iki nokta seçelim ve bunlara ${\displaystyle V}$ ve ${\displaystyle A}$ diyelim. ${\displaystyle VO}$ doğrusunu çizelim ve ${\displaystyle O}$'yu geçecek şekilde uzatalım, böylece ${\displaystyle V}$ noktasının çapa göre zıttı olan ${\displaystyle B}$ noktasında çemberle kesişir. Tepe noktası ${\displaystyle V}$ olan ve kenarları ${\displaystyle A}$ ve ${\displaystyle B}$ noktalarından geçen bir açı çizelim.

${\displaystyle OA}$ doğrusunu çizelim. Açı ${\displaystyle BOA}$, bir merkez açıdır; buna ${\displaystyle \theta }$ diyelim. ${\displaystyle OV}$ ve ${\displaystyle OA}$ çizgilerinin her ikisi de çemberin yarıçaplarıdır, bu nedenle eşit uzunluklara sahiptirler. Bu nedenle, ${\displaystyle \triangle VOA}$ üçgeni ikizkenardır, öyle ise ${\displaystyle \angle BVA}$ açısı (çevre açı) ve ${\displaystyle \angle VAO}$ açısı eşittir; her birini ${\displaystyle \psi }$ olarak gösterelim.

${\displaystyle \angle BOA}$ ve ${\displaystyle \angle AOV}$ açıları bütünlerdir. ${\displaystyle O}$'dan geçen ${\displaystyle VB}$ çizgisi düz bir doğru olana kadar toplamları ${\displaystyle 180^{\circ }}$'ye kadar artar. Bu nedenle, ${\displaystyle \angle AOV}$ açısının ölçüsü olarak ${\displaystyle 180^{\circ }-\theta }$ alınabilir.

Bir üçgenin üç açısının toplamının ${\displaystyle 180^{\circ }}$ olduğu ve ${\displaystyle \triangle VOA}$ üçgeninin üç açısının:

${\displaystyle {\text{açı}}_{1}=180^{\circ }-\theta }$

${\displaystyle {\text{açı}}_{2}=\psi }$

${\displaystyle {\text{açı}}_{3}=\psi }$.

Bu nedenle,

${\displaystyle 2\psi +180^{\circ }-\theta =180^{\circ }.}$

Her iki taraftan 180° çıkarırsak,

${\displaystyle 2\psi =\theta ,}$

burada ${\displaystyle \theta }$, ${\displaystyle AB}$ yayını gören merkez açı ve ${\displaystyle \psi }$, ${\displaystyle AB}$ yayını oluşturan çevre açıdır.

Çemberin merkezi, açının içinde kalan çevre açılar

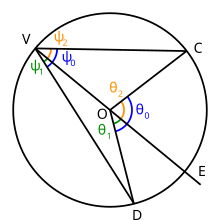
Merkezi ${\displaystyle O}$ noktası olan bir çember verildiğinde, çember üzerinde üç nokta ${\displaystyle V}$, ${\displaystyle C}$ ve ${\displaystyle D}$ alalım. ${\displaystyle VC}$ ve ${\displaystyle VD}$ doğrularını çizelim: ${\displaystyle \angle DVC}$ açısı, bir çevre açıdır. Şimdi ${\displaystyle VO}$ doğrusunu çizelim ve onu ${\displaystyle E}$ noktasında çemberle kesişecek şekilde ${\displaystyle O}$ noktasını geçecek şekilde uzatalım. ${\displaystyle \angle DVC}$ açısı, çember üzerindeki ${\displaystyle DC}$ yayını görür.

Bu yayın, içinde ${\displaystyle E}$ noktasını içerdiğini varsayalım. ${\displaystyle E}$ noktası, ${\displaystyle V}$ noktasının çapa göre karşısıdır. ${\displaystyle \angle DVE}$ ve ${\displaystyle \angle EVC}$ açıları da çevre açılardır, ancak bu açıların her ikisi de çemberin merkezinden geçen bir kenara sahiptir, bu nedenle yukarıdaki Bölüm 1'deki teorem bunlara uygulanabilir.

Bu nedenle,

${\displaystyle \angle DVC=\angle DVE+\angle EVC.}$

o zaman,

${\displaystyle \psi _{0}=\angle DVC,}$

${\displaystyle \psi _{1}=\angle DVE,}$

${\displaystyle \psi _{2}=\angle EVC,}$

Böylece

${\displaystyle \psi _{0}=\psi _{1}+\psi _{2}.\qquad \qquad (1)}$

${\displaystyle OC}$ ve ${\displaystyle OD}$ doğrularını çizelim. ${\displaystyle \angle DOE}$ ve ${\displaystyle \angle EOC}$ açıları gibi ${\displaystyle \angle DOC}$ açısı da merkezi bir açıdır ve

${\displaystyle \angle DOC=\angle DOE+\angle EOC.}$

${\displaystyle \theta _{0}=\angle DOC,}$

${\displaystyle \theta _{1}=\angle DOE,}$

${\displaystyle \theta _{2}=\angle EOC,}$

olsun, böylece

${\displaystyle \theta _{0}=\theta _{1}+\theta _{2}.\qquad \qquad (2)}$

Birinci bölümden biliyoruz ki ${\displaystyle \theta _{1}=2\psi _{1}}$ ve ${\displaystyle \theta _{2}=2\psi _{2}}$'dir. Bu sonuçların denklem (2) ile birleştirilmesi aşağıdaki sonucu verir:

${\displaystyle \theta _{0}=2\psi _{1}+2\psi _{2}=2(\psi _{1}+\psi _{2})}$

bu nedenle, denklem (1)'den aşağıdaki sonuç elde edilir:

${\displaystyle \theta _{0}=2\psi _{0}.}$

Çemberin merkezi, açının dışında kalan çevre açılar

Önceki durum, çevre açının ölçüsünün, bu ispatın ilk bölümünde tartışıldığı gibi iki çevre açı arasındaki fark olduğu durumu kapsayacak şekilde genişletilebilir.

Merkezi ${\displaystyle O}$ noktası olan bir çember verildiğinde, çember üzerinde üç nokta ${\displaystyle V}$, ${\displaystyle C}$ ve ${\displaystyle D}$ seçilsin. ${\displaystyle VC}$ ve ${\displaystyle VD}$ doğrularını çizelim: ${\displaystyle \angle DVC}$ açısı, bir çevre açıdır. Şimdi ${\displaystyle VO}$ doğrusunu çizelim ve ${\displaystyle E}$ noktasında çemberle kesişecek ve ${\displaystyle O}$ noktasını geçecek şekilde uzatalım. ${\displaystyle \angle DVC}$ açısı, çember üzerindeki ${\displaystyle DC}$ yayını görür.

Bu yayın, içinde ${\displaystyle E}$ noktasını içermediğini varsayalım. ${\displaystyle E}$ noktası, ${\displaystyle V}$ noktasının çapa göre zıttıdır. ${\displaystyle \angle EVD}$ ve ${\displaystyle \angle EVC}$ açıları da çevre açılardır, ancak bu açıların her ikisi de çemberin merkezinden geçen bir kenara sahiptir, bu nedenle yukarıdaki Bölüm 1'deki teorem bunlara uygulanabilir.

Bu nedenle,

${\displaystyle \angle DVC=\angle EVC-\angle EVD}$.

o zaman,

${\displaystyle \psi _{0}=\angle DVC,}$

${\displaystyle \psi _{1}=\angle EVD,}$

${\displaystyle \psi _{2}=\angle EVC,}$

olsun, böylece

${\displaystyle \psi _{0}=\psi _{2}-\psi _{1}.\qquad \qquad (3)}$

${\displaystyle OC}$ ve ${\displaystyle OD}$ doğrularını çizelim. ${\displaystyle \angle EOD}$ ve ${\displaystyle \angle EOC}$ açıları gibi ${\displaystyle \angle DOC}$ açısı da merkezi bir açıdır ve

${\displaystyle \angle DOC=\angle EOC-\angle EOD.}$

${\displaystyle \theta _{0}=\angle DOC,}$

${\displaystyle \theta _{1}=\angle EOD,}$

${\displaystyle \theta _{2}=\angle EOC,}$

olsun, böylece

${\displaystyle \theta _{0}=\theta _{2}-\theta _{1}.\qquad \qquad (4)}$

Birinci bölümden biliyoruz ki ${\displaystyle \theta _{1}=2\psi _{1}}$${\displaystyle \theta _{1}=2\psi _{1}}$ ve şu ${\displaystyle \theta _{2}=2\psi _{2}}$. Bu sonuçların denklem (4) ile birleştirilmesi,

${\displaystyle \theta _{0}=2\psi _{2}-2\psi _{1}}$

bu nedenle, denklem (3) ile aşağıdaki ifadeye ulaşılır:

${\displaystyle \theta _{0}=2\psi _{0}.}$

Sonuç

Benzer bir argümana göre, bir kiriş ile onun kesişme noktalarından birinde teğet doğrusu arasındaki açı, kirişin kapsadığı merkezi açının yarısına eşittir. Ayrıca bkz. Çemberlere teğet doğrular.

Uygulamalar

Çevre açı teoremi, düzlemin temel Öklid geometrisinin birçok ispatında kullanılır. Teoremin özel bir durumu, bir çapın kapsadığı açının her zaman ${\displaystyle 90^{\circ }}$, yani bir dik açı olduğunu belirten Thales teoremidir. Teoremin bir sonucu olarak, kirişler dörtgeninin zıt açılarının toplamı ${\displaystyle 180^{\circ }}$'dir ve tersine, bunun doğru olduğu herhangi bir dörtgen bir çember içerisine çizilebilir. Başka bir örnek olarak, çevre açı teoremi, bir çembere göre bir noktanın kuvveti ile ilgili birkaç teorem için temel oluşturur. Dahası, iki kiriş bir çember içinde kesiştiğinde, parçalarının uzunluklarının çarpımlarının eşit olduğunu kanıtlamaya izin verir.

Elipsler, hiperboller ve paraboller için çevre açı teoremleri

Çevre açı teoremleri elipsler, hiperboller ve paraboller için de mevcuttur. Temel farklar, bir açının ölçümleridir. (Bir açı, bir çift kesişen çizgi olarak kabul edilir.)

• Elips
• Hiperbol
• Parabol

Kaynakça

• Ogilvy, C. S. (1990). Excursions in Geometry. Dover. ss. 17-23. ISBN 0-486-26530-7. 
• Gellert W., Küstner H., Hellwich M., Kästner H. (1977). The VNR Concise Encyclopedia of Mathematics. New York: Van Nostrand Reinhold. s. 172. ISBN 0-442-22646-2. 
• Moise, Edwin E. (1974). Elementary Geometry from an Advanced Standpoint (2. bas.). Reading: Addison-Wesley. ss. 192-197. ISBN 0-201-04793-4. 

Dış bağlantılar

• Eric W. Weisstein, Inscribed Angle (MathWorld)
• "Relationship Between Central Angle and Inscribed Angle". 11 Mayıs 2009 tarihinde kaynağından arşivlendi. 
• "Munching on Inscribed Angles". cut-the-knot.org. 15 Nisan 2003 tarihinde kaynağından arşivlendi. 
• "Arc Central Angle". 30 Ekim 2006 tarihinde kaynağından arşivlendi. (etkileşimli animasyon ile) 
• "Arc Peripheral (inscribed) Angle". 30 Ekim 2006 tarihinde kaynağından arşivlendi. (etkileşimli animasyon ile) 
• "Arc Central Angle Theorem". 30 Ekim 2006 tarihinde kaynağından arşivlendi. (etkileşimli animasyon ile) 
• "Inscribed angle theorem". bookofproofs.org. 11 Temmuz 2020 tarihinde kaynağından arşivlendi.