Série convergente

Em matemática, uma série é o somatório dos termos de uma sequência de números.

Dada uma sequência infinita ${\displaystyle (a_{1},a_{2},a_{3},\dots )}$, a ${\displaystyle n}$-ésima soma parcial ${\displaystyle S_{n}}$ é a soma dos primeiros termos da sequência, isto é,

${\displaystyle S_{n}=\sum _{k=1}^{n}a_{k}.}$

Uma série é convergente se a sequência de suas somas parciais ${\displaystyle \{S_{1},S_{2},S_{3},\dots \}}$ tende a um limite. Isto quer dizer que as somas parciais se tornam cada vez mais próximas de um dado número quando o número de seus termos aumenta. Em uma linguagem mais formal, uma série converge se existe um limite ${\displaystyle \ell }$ tal que para qualquer número positivo arbitrariamente pequeno ${\displaystyle \varepsilon >0}$, existe um inteiro ${\displaystyle N}$ tal que para todo ${\displaystyle n\geq \ N}$,

${\displaystyle |S_{n}-\ell |\leq \varepsilon .}$

Qualquer série que não é convergente é chamada de divergente.^[1]

Exemplos de séries convergentes e divergentes

• Os inversos dos inteiros positivos produzem uma série divergente (série harmônica):

${\displaystyle {1 \over 1}+{1 \over 2}+{1 \over 3}+{1 \over 4}+{1 \over 5}+{1 \over 6}+\cdots \rightarrow \infty .}$

• Alternar os sinais dos inversos dos inteiros positivos produz uma série convergente:

  ${\displaystyle {1 \over 1}-{1 \over 2}+{1 \over 3}-{1 \over 4}+{1 \over 5}-{1 \over 6}+\cdots =\ln 2.}$

• Alternar os sinais dos inversos dos inteiros ímpares produz uma série convergente (a Fórmula de Leibniz para ${\displaystyle \pi }$):

  ${\displaystyle {1 \over 1}-{1 \over 3}+{1 \over 5}-{1 \over 7}+{1 \over 9}-{1 \over 11}+\cdots ={\pi \over 4}.}$

• Os inversos dos números primos produzem uma série divergente (assim sendo, o conjunto dos primos é "grande"):

${\displaystyle {1 \over 2}+{1 \over 3}+{1 \over 5}+{1 \over 7}+{1 \over 11}+{1 \over 13}+\cdots \rightarrow \infty .}$

• Os inversos dos números triangulares produzem uma série convergente:

  ${\displaystyle {1 \over 1}+{1 \over 3}+{1 \over 6}+{1 \over 10}+{1 \over 15}+{1 \over 21}+\cdots =2.}$

• Os inversos dos fatoriais produzem uma série convergente (ver número de Euler ${\displaystyle e}$):

  ${\displaystyle {\frac {1}{1}}+{\frac {1}{1}}+{\frac {1}{2}}+{\frac {1}{6}}+{\frac {1}{24}}+{\frac {1}{120}}+\cdots =e.}$

• Os inversos dos números quadrados produzem uma série convergente (o Problema de Basileia):

  ${\displaystyle {1 \over 1}+{1 \over 4}+{1 \over 9}+{1 \over 16}+{1 \over 25}+{1 \over 36}+\cdots ={\pi ^{2} \over 6}.}$

• Os inversos das potências de 2 produzem uma série convergente (assim sendo, o conjunto das potências de 2 é "pequeno"):

  ${\displaystyle {1 \over 1}+{1 \over 2}+{1 \over 4}+{1 \over 8}+{1 \over 16}+{1 \over 32}+\cdots =2.}$

• Os inversos das potências de qualquer ${\displaystyle n}$ produzem uma série convergente:

  ${\displaystyle {1 \over 1}+{1 \over n}+{1 \over n^{2}}+{1 \over n^{3}}+{1 \over n^{4}}+{1 \over n^{5}}+\cdots ={n \over n-1}.}$

• Alternar os sinais dos inversos das potências de 2 também produz uma série convergente:

  ${\displaystyle {1 \over 1}-{1 \over 2}+{1 \over 4}-{1 \over 8}+{1 \over 16}-{1 \over 32}+\cdots ={2 \over 3}.}$

• Alternar os sinais dos inversos das potências de qualquer ${\displaystyle n}$ produz uma série convergente:

  ${\displaystyle {1 \over 1}-{1 \over n}+{1 \over n^{2}}-{1 \over n^{3}}+{1 \over n^{4}}-{1 \over n^{5}}+\cdots ={n \over n+1}.}$

• Os inversos dos números de Fibonacci produzem uma série convergente, sendo ${\displaystyle \psi }$ a constante dos inversos de Fibonacci:

  ${\displaystyle {1 \over 1}-{1 \over 1}+{1 \over 2}-{1 \over 3}+{1 \over 5}-{1 \over 8}+\cdots =\psi .}$^[2]

Testes de convergência

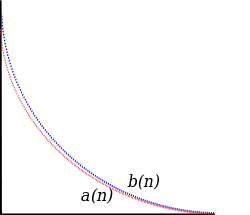
Existem alguns métodos para determinar se uma série converge ou diverge.

• Teste da comparação: Os termos da sequência ${\displaystyle \left\{a_{n}\right\}}$ são comparados àqueles de outra sequência ${\displaystyle \left\{b_{n}\right\}}$. Se,

para todo ${\displaystyle n}$, ${\displaystyle 0\leq a_{n}\leq b_{n}}$ e ${\displaystyle \sum _{n=1}^{\infty }b_{n}}$ converge, então o mesmo acontece com ${\displaystyle \sum _{n=1}^{\infty }a_{n}.}$ Contudo, se, para todo ${\displaystyle n}$, ${\displaystyle 0\leq b_{n}\leq a_{n}}$ e ${\displaystyle \sum _{n=1}^{\infty }b_{n}}$ diverge, então o mesmo acontece com ${\displaystyle \sum _{n=1}^{\infty }a_{n}.}$

• Teste da razão: Assuma que para todo ${\displaystyle n}$, ${\displaystyle a_{n}>0}$. Suponha que existe ${\displaystyle r}$ tal que:

  ${\displaystyle \lim _{n\to \infty }{\frac {a_{n+1}}{a_{n}}}=r.}$

Se ${\displaystyle r<1}$, então a série converge. Se ${\displaystyle r>1}$, então a série diverge. Se ${\displaystyle r=1}$, o teste da razão é inconclusivo e a série pode convergir ou divergir.

• Teste da raiz ou teste da raiz ${\displaystyle n}$-ésima: Suponha que os termos da sequência em questão são números não negativos. Defina ${\displaystyle r}$ como se segue:

  ${\displaystyle r=\limsup _{n\rightarrow \infty }{\sqrt[{n}]{|a_{n}|}},}$

em que ${\displaystyle \limsup }$ denota o limite superior (possivelmente ${\displaystyle \infty }$; se o limite existir, é o mesmo valor).

Se ${\displaystyle r<1}$, então a série converge. Se ${\displaystyle r>1}$, então a série diverge. Se ${\displaystyle r=1}$, o teste da raiz é inconclusivo e a série pode convergir ou divergir.

O teste da razão e o teste da raiz são ambos baseados na comparação com uma série geométrica e, como tal, funcionam em situações similares. De fato, se o teste da razão funcionar (significando que o limite existe e não é igual a 1), então o mesmo acontece com o teste da raiz. O inverso, porém, não é verdadeiro. Por isso, o teste da raiz é de aplicação mais geral, mas, em termos práticos, é frequentemente difícil computar o limite para tipos de séries comumente encontrados.

• Teste da P-Séries : Uma importante classe de séries numéricas é quando são constituída da série da seguinte forma ${\displaystyle \sum _{n=1}^{\infty }{1 \over n^{p}}}$
  este tipo de série é conhecido com p-séries e que são bastante utilizado com série de prova nos critérios de comparação. Observe que o termo geral ${\displaystyle a_{n}=1/n^{p}}$ tem limite 1, quando ${\displaystyle p=0}$, e limite é infinito quando ${\displaystyle p<0}$ e em ambos os casos a série é divergente. Se ${\displaystyle p=1}$ temos então a série harmônica, que neste caso também é divergente. Nos demais casos a convergência das p-séries será analisado pelo critério de Integral. Quando a função ${\displaystyle f(x)=1/x^{p}}$ e ${\displaystyle p>0}$ e ${\displaystyle x}$ é maior ou igual a 1, temos então duas condições:

${\displaystyle {\text{caso 1}}:}$ Se ${\displaystyle 0<p<1}$,

${\displaystyle \int _{1}^{\infty }f(x)\,dx{\text{ (Diverge)}}}$

${\displaystyle {\text{caso 2}}:}$ Se ${\displaystyle p>1}$,

${\displaystyle \int _{1}^{\infty }f(x)\,dx{\text{ (Converge)}}}$

A integral imprópria quando ${\displaystyle p>1}$ é convergente, consequentemente é o único caso que p-série ${\displaystyle \sum _{n=1}^{\infty }{1 \over n^{p}}}$ é também converge.

Exemplos :

Convergentes ${\displaystyle \sum _{n=1}^{\infty }{1 \over n^{5/2}}}$ e ${\displaystyle \sum _{n=1}^{\infty }{1 \over n^{2}}}$

Divergentes ${\displaystyle \sum _{n=1}^{\infty }{1 \over n}}$ e ${\displaystyle \sum _{n=1}^{\infty }{1 \over n^{2/3}}}$

• Teste da integral: A série pode ser comparada com uma integral para estabelecer convergência ou divergência. Considere ${\displaystyle f(n)=a_{n}}$ uma função positiva e monotonicamente decrescente. Se

  ${\displaystyle \int _{1}^{\infty }f(x)dx=\lim _{t\to \infty }\int _{1}^{t}f(x)dx<\infty ,}$

então a série converge. No entanto, se a integral diverge, o mesmo acontece com a série.

• Teste da comparação do limite: Se ${\displaystyle \{a_{n}\},\{b_{n}\}>0}$, o limite ${\displaystyle \lim _{n\to \infty }{\frac {a_{n}}{b_{n}}}}$ existir e for diferente de zero, então ${\displaystyle \sum _{n=1}^{\infty }a_{n}}$ converge se e somente se ${\displaystyle \sum _{n=1}^{\infty }b_{n}}$ convergir.
• Teste da série alternada: Também conhecido como critério de Leibniz, o teste da série alternada estabelece que para uma série alternada da forma ${\displaystyle \sum _{n=1}^{\infty }a_{n}(-1)^{n}}$, se ${\displaystyle \{a_{n}\}}$ for monotonicamente decrescente e tiver um limite zero no infinito, então a série converge.
• Teste da condensação de Cauchy: Se ${\displaystyle \{a_{n}\}}$ for uma sequência monotonicamente decrescente positiva, então ${\displaystyle \sum _{n=1}^{\infty }a_{n}}$ converge se e somente se ${\displaystyle \sum _{k=1}^{\infty }2^{k}a_{2^{k}}}$ convergir.

Outros exemplos incluem o teste de Dirichlet, o teste de Abel e o teste de Raabe.^[3]

Convergência condicional e absoluta

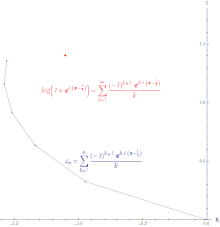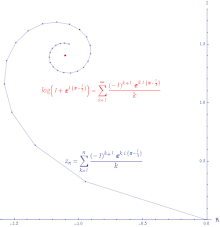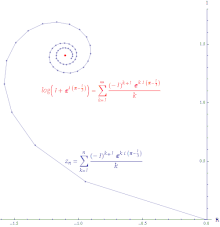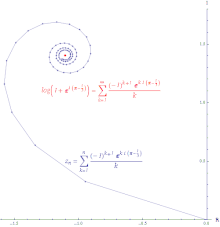
Para qualquer sequência ${\displaystyle \{a_{1},a_{2},a_{3},\dots \}}$, ${\displaystyle a_{n}\leq |a_{n}|}$ para todo ${\displaystyle n}$. Por isso,

${\displaystyle \sum _{n=1}^{\infty }a_{n}\leq \sum _{n=1}^{\infty }|a_{n}|.}$

Isto significa que, se ${\displaystyle \sum _{n=1}^{\infty }|a_{n}|}$ convergir, então ${\displaystyle \sum _{n=1}^{\infty }a_{n}}$ também converge (mas não vice-versa).

Se a série ${\displaystyle \sum _{n=1}^{\infty }|a_{n}|}$ convergir, então, a série ${\displaystyle \sum _{n=1}^{\infty }a_{n}}$ é absolutamente convergente. Um sequência absolutamente convergente é uma sequência na qual a linha criada ao juntar todos os incrementos à soma parcial é finitamente longa. A série das potências da função exponencial é absolutamente convergente em todo lugar.

Se a série ${\displaystyle \sum _{n=1}^{\infty }a_{n}}$ convergir, mas a série ${\displaystyle \sum _{n=1}^{\infty }|a_{n}|}$ divergir, então a série ${\displaystyle \sum _{n=1}^{\infty }a_{n}}$ é condicionalmente convergente. O caminho formado ao conectar as somas parciais de uma série condicionalmente convergente é infinitamente longo. A série das potências do logaritmo é condicionalmente convergente.

O teorema das séries de Riemann afirma que, se uma série convergir condicionalmente, é possível rearranjar os termos da série de tal maneira que a série converge a qualquer valor ou até mesmo diverge.^[4]

Convergência uniforme

Considere ${\displaystyle \{f_{1},f_{2},f_{3},\dots \}}$ uma sequência de funções. Diz-se que a série ${\displaystyle \sum _{n=1}^{\infty }f_{n}}$ converge uniformemente a ${\displaystyle f}$ se a sequência ${\displaystyle \{s_{n}\}}$ de somas parciais definida por:

${\displaystyle s_{n}(x)=\sum _{k=1}^{n}f_{k}(x)}$

convergir uniformemente a ${\displaystyle f}$.

Há um análogo do teste de comparação para séries infinitas de funções chamado teste M de Weierstrass.^[5]

Critério de convergência de Cauchy

O critério de convergência de Cauchy afirma que uma série ${\displaystyle \sum _{n=1}^{\infty }a_{n}}$ converge se e apenas se a sequência de somas parciais for uma sequência de Cauchy.

Isto significa que, para todo ${\displaystyle \varepsilon >0}$, há um número inteiro positivo ${\displaystyle N}$ tal que, para ${\displaystyle n\geq m\geq N}$, temos:

${\displaystyle \left|\sum _{k=m}^{n}a_{k}\right|<\varepsilon ,}$

que é equivalente a:

${\displaystyle \lim _{n\to \infty \atop m\to \infty }\sum _{k=n}^{n+m}a_{k}=0.}$^[6]

Ver também

• Limite de uma sequência
• Série divergente

Referências

^[1]

• Portal da matemática