定和

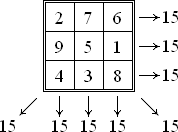
魔方陣の定和（ていわ）とは、各列の数字の合計の値である。立方陣・魔六角陣・星陣などの同種のパズルにもこの語が使用される。魔方陣の性質より特定の魔方陣における定和は一定の値となる。

魔方陣の定和

n次の魔方陣には 1–n² の数が入るのでその合計は ${\frac {n^{2}(n^{2}+1)}{2}}$ である。この中には独立した n個の列があるため n次の魔方陣の定和は以下の式で表される。

{\frac {n(n^{2}+1)}{2}}

具体的には n≥3 で 15, 34, 65, …（オンライン整数列大辞典の数列 A6003）となる。n=2 のときの値も計算はできるが、この大きさの魔方陣は存在しないので意味を持たない。

素数方陣のように1からの連続数を使用しない方陣の場合の定和は「（使用した数字の総和）÷（列の数）」で求めることができる。

一般的な魔方陣の場合は縦横の列及び対角線の合計のみが定和となるが、フランクリン方陣や汎魔方陣の場合はそれ以外の場所の和が定和になることもある。例えば5次の汎魔方陣では、任意のマスとそれに隣接する4マスの数の合計が定和と等しくなる。

その他の場合の定和

n次の立方陣の定和は同様に計算すると ${\frac {n(n^{3}+1)}{2}}$ となる。

1から始まる数字で作った1辺の長さがnの魔六角陣の定和は ${\frac {(3n^{2}-3n+1)(3n^{2}-3n+2)}{2(2n-1)}}$ である。これが整数になるのは n=1,3 のときのみである。mから始まる数字で作った場合の定和は ${\frac {9n^{4}-18n^{3}+6(m+2)n^{2}-3(2m+1)n+2m}{2(2n-1)}}$ となる。