四次函数

3つの極値を持つ四次多項式関数のグラフ

数学において、四次関数（よじかんすう、英: quartic function, biquadratic function[注 1]）は、次数 4 の多項式の定める関数である。一変数の場合には具体的に、a (≠ 0) および b, c, d を定数として

f ( x ) = a x 4 + b x 3 + c x 2 + d x + e {\displaystyle f(x)=ax^{4}+bx^{3}+cx^{2}+dx+e}

と表される。特別の場合として、x2 の二次関数：

f ( x ) = a x 4 + b x 2 + c {\displaystyle f(x)=ax^{4}+bx^{2}+c}

を複二次関数 (biquadratic function)[注 1]と呼ぶ。

四次関数 f(x) の零点（x切片）は四次方程式

f ( x ) = a x 4 + b x 3 + c x 2 + d x + e = 0 ( a ≠ 0 ) {\displaystyle f(x)=ax^{4}+bx^{3}+cx^{2}+dx+e=0\quad (a\neq 0)}

の解である。また、四次関数の導関数は三次関数になる。

四次関数は偶数次の多項式関数だから、変数を正の無限大 +∞ に近づける極限でも、負の無限大 −∞ に近づける極限でも、ともに等しい極限を持つ。この極限は、最高次の係数 a が正ならば、正の無限大となり、従ってその四次関数は（大域的な）最小値を持つ。同じように、a が負ならば負の無限大へ発散し、（大域的な）最大値を持つ。

応用

高次多項式関数は最適化問題にしばしば現れ、それは時に四次多項式だったりもするが、それはたまたまそうなるだけである。

コンピュータグラフィックでは、二次曲面やトーラス面（これは球面や可展面などの次のレベルの曲面）に対するレイトレーシングなどに四次函数が現れる。

二つの楕円の交点などを考えても四次式が現れる。

計算機支援製造 (computer-aided manufacturing; CAM) では、エンドミルカッターの形状としてトーラスがよく見られる。三角形分割された曲面に関する位置関係を計算するには、z軸上に置かれた水平トーラスの位置を、接面を固定した状態で求めなければならず、これには四次方程式を解く必要が生じる。CAMにおける計算時間の10％以上は単に数百万の四次方程式の解を計算することに費やされている。

A program demonstrating various analytic solutions to the quartic was provided in Graphics Gems Book V.[1] However, none of the three algorithms implemented are unconditionally stable. In an updated version of the paper,[2] which compares the 3 algorithms from the original paper and 2 others, it is demonstrated that computationally stable solutions exist only for 4 of the possible 16 sign combinations of the quartic coefficients.

性質

重根の存在を調べる四次式の判別式は、定義通り根の差積の平方（にヴィエタの公式を代入したもの）として計算すると、16個の項をもつかなり複雑な式となる。したがって、数値計算する上では簡潔な行列式としてまとまる判別式の終結式による表現が有用である。すなわち、

Q ( x ) = a x 4 + b x 3 + c x 2 + d x + e {\displaystyle Q(x)=ax^{4}+bx^{3}+cx^{2}+dx+e}

の判別式 DQ は

D Q = − R e s ( Q , Q ′ ) = − | a b c d e 0 0 0 a b c d e 0 0 0 a b c d e 4 a 3 b 2 c d 0 0 0 0 4 a 3 b 2 c d 0 0 0 0 4 a 3 b 2 c d 0 0 0 0 4 a 3 b 2 c d | {\displaystyle D_{Q}=-\mathrm {Res} (Q,Q')=-{\begin{vmatrix}a&b&c&d&e&0&0\\0&a&b&c&d&e&0\\0&0&a&b&c&d&e\\4a&3b&2c&d&0&0&0\\0&4a&3b&2c&d&0&0\\0&0&4a&3b&2c&d&0\\0&0&0&4a&3b&2c&d\end{vmatrix}}}

となる。

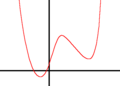
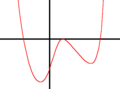
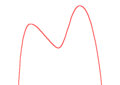
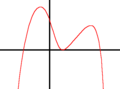
四次関数のグラフの概形は、最高次係数の正負、重根・三重根・四重根の有無、導函数の零点の有無、導函数の重根・三重根の有無などにより分類することができる。

四次方程式との関係

詳細は「四次方程式」を参照

四次関数の根は代数的な表示を持つ。四次函数の根の表示を求める方法については四次方程式の項を参照。

四次関数がより低次の多項式に何らかの意味で帰着できるならば、その性質の理解は幾分容易になる。四次函数

Q ( x ) = a 4 x 4 + a 3 x 3 + a 2 x 2 + a 1 x + a 0 {\displaystyle Q(x)=a_{4}x^{4}+a_{3}x^{3}+a_{2}x^{2}+a_{1}x+a_{0}}

が例えば、因数分解されているとか、適当な変数変換で低次の方程式になる場合などが典型である。因数定理によれば、方程式 Q(x) = 0 を解いて零点を知れば因数分解をすることができるし、四次方程式におけるフェラリの解法などは分解方程式と呼ばれる低次の方程式に帰着する方法を取っている。

例えば、四次の準相反方程式

a 0 x 4 + a 1 x 3 + a 2 x 2 + a 1 m x + a 0 m 2 = 0 {\displaystyle a_{0}x^{4}+a_{1}x^{3}+a_{2}x^{2}+a_{1}mx+a_{0}m^{2}=0}

は x2 で両辺を割って、変数変換 z = x + m/x を行えば、z の二次方程式となるから、それを解いてもとへ返せば因数分解ができる。

脚注・参照

脚注
  1. ^ a b biquadratic function という語は、四次関数の意味でも複二次式の意味でも使われるため紛らわしい。

参照

  1. ^ http://www.acm.org/pubs/tog/GraphicsGems/gems.html#gemsv
  2. ^ http://www-staff.it.uts.edu.au/~don/pubs/solving.html

参考文献

  • Faucette, William Mark (1996), “A Geometric Interpretation of the Solution of the General Quartic Polynomial”, The American Mathematical Monthly 103 (1): 51-57, doi:10.2307/2975214, http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.111.5574&rep=rep1&type=pdf 
  • Nickalls, R. W. D. (2009). “The quartic equation: invariants and Euler's solution revealed”. Mathematical Gazette 93: 66-75. http://www.nickalls.org/dick/papers/maths/quartic2009.pdf. 
  • Carpenter, W. (1966). “On the solution of the real quartic”. Mathematics Magazine 39: 28-30. 
  • Brookfield, G. (2007). “Factoring quartic polynomials: A lost art”. Mathematics Magazine 80 (1): 67-70. 

外部リンク

  • 表
  • 話
  • 編
  • 歴
元数
次数
多項式
函数
方程式
項数
係数条件
アルゴリズム
関連項目
カテゴリ カテゴリ