Görbület

A görbület matematikai, azon belül geometriai fogalom. Szemléletesen egy sík- vagy térgörbe egyenestől való eltérését, illetve egy térbeli felületnek a síktól való eltérését jellemző számérték.

A görbék és a felületek görbületének definíciója eltérő, az utóbbi az előbbire támaszkodik.

Görbék görbülete

Görbület

Az ábrán s-sel jelölt görbén irányítást definiálunk, s ennek megfelelően értelmezzük a görbe egy-egy pontjában húzott érintő irányát: érintővektor. A görbe egy BC irányított ívéhez tartozó átlagos görbület (v.ö.: átlagsebesség) a két végponthoz tartozó érintővektorok szögének és az s = BC ívhossznak a hányadosa:

${\displaystyle \ g={\frac {\Delta \alpha }{\Delta s}}}$

A görbe egy pontjában értelmezett görbület e hányados határértéke, midőn az ívhossz 0-hoz tart (s → 0, azaz C → B).

${\displaystyle \ g=\lim {\frac {\Delta \alpha }{\Delta s}}={\frac {d\alpha }{ds}}}$

Másként fogalmazva: A pontbeli görbület az érintő irányváltozásának a pályamenti sebessége, az irányszög ívhossz szerinti első deriváltja.

Görbületi sugár, simulókör

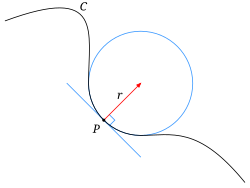
A görbe három (nem egy egyenesbe eső) pontja mindig meghatároz egy síkot (síkgörbe esetén a befoglaló síkot) és e síkban egy kört. Az ú.n. simulókört (görbületi kört) kapjuk, ha a három pont egyetlen pontba konvergál. E kör sugara a görbe adott pontjához tartozó görbületi sugár.

• A simulókör sugara a görbület reciproka:

${\displaystyle r={\frac {1}{\ g}}\,}$,

• A simulókörök középpontjának mértani helye a görbe evolutája.
• A görbén egyenletes v pályamenti sebességgel haladó m tömegű testre ható centripetális erő pontonként változó:

${\displaystyle {\vec {F}}=m{\vec {g}}v^{2}}$.

• Az egyenes vonal görbülete 0, az r sugarú kör görbülete 1/r minden pontban. E két síkgörbe (és csak ezek) állandó görbületűek. A térben ilyen a körhenger felületére illeszkedő, állandó emelkedésű csavarvonal.

A görbület számítása

Ha a görbe egy analitikus függvény grafikonja és egyenlete

${\displaystyle y=f(x)\,}$,

alakban adott, akkor a görbület:

${\displaystyle g={\frac {y''}{(1+y'^{2})^{3/2}}}}$.

Ha a síkgörbe egyenlete az alábbi parametrikus formában adott:

${\displaystyle {\begin{cases}x=x(t)\\y=y(t)\end{cases}}}$

${\displaystyle g(t)={\frac {{\dot {x}}{\ddot {y}}-{\dot {y}}{\ddot {x}}}{({\dot {x}}^{2}+{\dot {y}}^{2})^{3/2}}}}$.

Ha a görbe egyenlete ${\displaystyle r(\theta )\,}$ polárkoordinátákkal adott, görbülete:

${\displaystyle g(\theta )={\frac {r^{2}+2r'^{2}-rr''}{\left(r^{2}+r'^{2}\right)^{3/2}}}}$,

ahol a vessző (') a ${\displaystyle \theta \,}$ szerinti deriváltat jelöli.

A görbe egyenlete megadható parametrikus polárkoordinátákkal is:

${\displaystyle {\begin{cases}r=r(t)\\\theta =\theta (t)\end{cases}}}$

Ekkor a görbület

${\displaystyle g={\frac {{\dot {\theta }}(2{\dot {r}}^{2}+r^{2}{\dot {\theta }}^{2})+r({\dot {r}}{\ddot {\theta }}-{\dot {\theta }}{\ddot {r}})}{({\dot {r}}^{2}+r^{2}{\dot {\theta }}^{2})^{3/2}}}}$.

Ha a görbe egyenlete implicit alakban adott:

${\displaystyle F(x,y)=0\,}$, akkor a görbület:

${\displaystyle g={\frac {\begin{vmatrix}F_{xx}''&F_{xy}''&F_{x}'\\F_{yx}''&F_{yy}''&F_{y}'\\F_{x}'&F_{y}'&0\\\end{vmatrix}}{(F_{x}'^{2}+F_{y}'^{2})^{3/2}}}}$

Térgörbék görbülete

Paraméteresen adott térgörbe görbülete:

${\displaystyle g={\frac {\sqrt {(z''y'-y''z')^{2}+(x''z'-z''x')^{2}+(y''x'-x''y')^{2}}}{(x'^{2}+y'^{2}+z'^{2})^{3/2}}}}$

Ha a görbe ${\displaystyle r(t)\,}$ helyvektorának függvényével adott, akkor a görbület:

${\displaystyle g={\frac {|{\dot {r}}\times {\ddot {r}}|}{|{\dot {r}}|^{3}}}.}$

Felületek görbülete

A felület egy P pontjában a görbültségét (síktól való eltérését) a ponton átmenő jellegzetes felületi görbék görbületének értékével jellemezhetjük. A felületi görbület definíciójánál a P pontra illeszkedő síkmetszetek, s ezek közül csak az ú.n. normálmetszetek görbületét vesszük figyelembe.

Normálmetszet

A felület P pontbeli C normálmetszetét (felületi görbét) a felület adott pontbeli normálvektorát tartalmazó sík metszi ki. Egy ilyen normálmetszet görbülete a metszősík helyzetétől függ:

${\displaystyle {\vec {g}}={\frac {1}{R}}}$.

A metszősíkot a normálvektor egyenese körül elforgatva az R₁ = R_max és R₂ = R_min értékekhez tartozó C₁ és C₂ metszetek az adott P ponthoz tartozó főnormálmetszetek.

Euler képlete

A C₁ főnormálmetszet síkjával α szöget bezáró C normálmetszet görbülete a főnormálmetszetek görbületével kifejezve:

${\displaystyle g=g_{1}cos^{2}\alpha +g_{2}sin^{2}\alpha }$

..azaz..

${\displaystyle {\frac {1}{R}}={\frac {cos^{2}\alpha }{R_{1}}}+{\frac {sin^{2}\alpha }{R_{2}}}}$.

Gauss-féle görbület

A P ponthoz tartozó két főnormálmetszet görbületi sugarával kifejezve:

${\displaystyle G=g_{1}.g_{2}={\frac {1}{R_{1}R_{2}}}}$.

Középgörbület

A P ponthoz tartozó két főnormálmetszet görbületének számtani közepe:

${\displaystyle H={\frac {g_{1}+g_{2}}{2}}={\frac {1}{2}}\left({\frac {1}{R_{1}}}+{\frac {1}{R_{2}}}\right)}$.

Források

• Pattantyús Gépész- és Villamosmérnökök Kézikönyve 1. kötet. Műszaki Könyvkiadó, Budapest, 1961.
• Bronstejn-Szemengyajev: Matematikai zsebkönyv. Műszaki Könyvkiadó, Budapest, 1963.
• Pach Zs. Pálné - Frey Tamás: Vektor- és tenzoranalízis, Műszaki könyvkiadó, Budapest, 1964.