Rolleren teorema

Kalkulu diferentzialean, Rolle-ren teoremak dio funtzio bat ${\displaystyle [a,b]}$ tarte batean jarraia eta ${\displaystyle (a,b)}$ tarte batean deribagarria bada, ${\displaystyle f(a)=f(b)}$ izanik, existituko dela gutxienez puntu bat tarte horretan malda nulua duena, hau da, ${\displaystyle \exists c\in (a,b):f'(c)=0}$. Bataz besteko balioaren teoremaren kasu berezi bat da.

Bhaskara II matematikari indiarrak deskribatu zuen 12. mendean, baina Michel Rolle (1652-1719) matematikariak frogatu zuen 1691-an.

Teorema

Izan bedi ${\displaystyle f}$ funtzioa ${\displaystyle [a,b]}$ tartean jarraitua eta ${\displaystyle (a,b)}$ tarte irekian deribagarria eta demagun ${\displaystyle f(a)=f(b)}$ dela. Orduan ${\displaystyle \exists c\in (a,b):f'(c)=0}$.

Froga

${\displaystyle f}$ funtzioa ${\displaystyle [a,b]}$ tartean jarraitua denez, minimo eta maximo absolutuak lortzen ditu ${\displaystyle [a,b]}$ tartean arabera, hau da, ${\displaystyle f(x_{0})\leq f(x)\leq f(y_{0}),\forall x\in [a,b]}$. Bi posibilitate daude:

• Maximoa edo minimoa ${\displaystyle (a,b)}$ tartean dago. ${\displaystyle x_{0}}$ puntua orduan mutur bat (minimo bat) izango da, beraz ${\displaystyle f'(x_{0})=0}$, mutur baten deribatuaren balioa ${\displaystyle 0}$ delako, eta ${\displaystyle c=x_{0}}$ izango da. ${\displaystyle y_{0}}$ puntuaren kasuan konklusioa berdina da.
• Aurrekoa ez bada egia, ${\displaystyle x_{0}}$ eta ${\displaystyle y_{0}}$ tartearen muturrak izango dira. Beraz, ${\displaystyle a={\displaystyle x_{0}}}$ eta ${\displaystyle b={\displaystyle y_{0}}}$ suposatu dezakegu. Beraz, ${\displaystyle f(x_{0})\leq f(x)\leq f(y_{0}),\forall x\in [a,b]}$ ikusi dezakegu, baina ${\displaystyle a=b}$ denez, funtzioa konstantea izango da, eta edozein punturen deribatuaren balioa ${\displaystyle 0}$ izango da.

Adierazpen geometrikoa

Hurrengo irudian ikus daitekeenez, hiru baldintzak betetzen dira: funtzioa ${\displaystyle [a,b]}$ tarte batean jarraitua da, ${\displaystyle (a,b)}$ tarte batean deribagarria eta ${\displaystyle f(a)=f(b)}$ da. Ikus daitekeenez, badago gutxienez ${\displaystyle c}$ puntu bat non ${\displaystyle f'(c)=0}$, kasu honetan puntu guztiak, funtzioa konstantea delako.

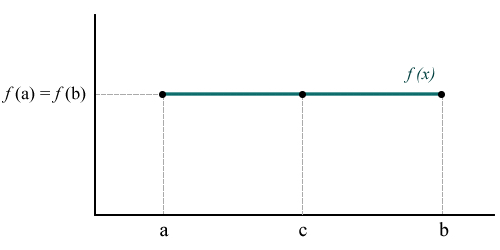
Irudian funtzio konstantea ikus daiteke, baina ez da betetzen den kasu bakarra.

1. kasua

Hurrengo kasuan ikus daitekeenez, tartearen puntu maximoa ${\displaystyle f(a)}$ eta ${\displaystyle f(b)}$-ren berdina da, eta minimoa ezberdina da, beraz, kurba ganbila da.. Puntu minimoa ${\displaystyle {\displaystyle m=f(c)}}$ da, eta funtzioaren deribatua puntu honetan ${\displaystyle 0}$ da.

2. kasua

Puntu minimoa ${\displaystyle f(a)}$ eta ${\displaystyle f(b)}$-ren berdina da eta maximoa ezberdina, beraz, kurba ahurra da. Puntu maximoa ${\displaystyle M=f(c)}$ da eta bere deribatua ${\displaystyle 0}$ da puntu horretan.

3. kasua

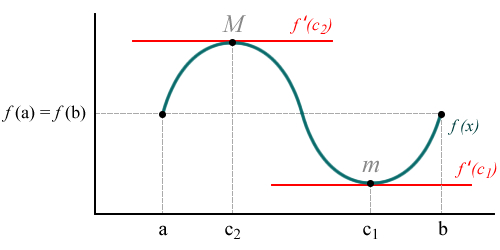
Kasu honetan, bai puntu maximo bai minimoa ${\displaystyle f(a)}$ eta ${\displaystyle f(b)}$-ren ezberdinak dira. Beraz, funtzioak ${\displaystyle [a,b]}$ tarte barnean ${\displaystyle f(a)}$ eta ${\displaystyle f(b)}$ baino handiagoa den ${\displaystyle M=f(c_{2})}$ puntu maximo bat eta ${\displaystyle f(a)}$ eta ${\displaystyle f(b)}$ baino txikiagoa den ${\displaystyle m=f(c_{1})}$ puntu bat izango ditu gutxienez. Bai maximoan bai minimoan deribatuaren balioa nulua izango da, hau da,${\displaystyle f'(c_{1})=0}$ eta ${\displaystyle f'(c_{2})=0}$.

Kanpo estekak

• Datuak: Q193286
• Multimedia: Rolle's theorem / Q193286