Relación binaria

Una relación binaria R es el subconjunto de los elementos del producto cartesiano ${\displaystyle A_{1}\times A_{2}\ }$ que cumplen una determinada condición:

${\displaystyle R=\{(a_{1},a_{2}):\;(a_{1},a_{2})\in A_{1}\times A_{2}\;\land \;R(a_{1},a_{2})=Verdadero\}}$

Taxonomía de las relaciones binarias

En el gráfico ilustrativo de la taxonomía de las relaciones binarias se pasa de las definiciones más generales a las más específicas siguiendo el sentido dependiente de las flechas.

Clasificación

La importancia en matemáticas de las relaciones binarias, se debe a que una gran parte de las asociaciones entre elementos de conjuntos, tanto numéricos como no numéricos, se hace de dos en dos elementos, tanto si son elementos de un único conjunto o de dos conjuntos distintos, en el esquema se puede ver algunas estructuras algebraicas o subtipos de relación binaria. Emplearemos este esquema para ver estos casos.

En primer lugar diferenciamos las relaciones binarias homogéneas, de las heterogéneas. En las primeras, la relación binaria se establece entre los elementos de un único conjunto, por lo que en realidad, lo que determina es su estructura interna, mientras que en las segundas se establecen relaciones entre dos conjuntos distintos, lo que da lugar a operaciones o funciones matemáticas de cálculo. Una relación homogénea puede ser tratada como heterogénea con los mismos subtipos, pero no al contrario.

Relación homogénea

Una relación binaria R es homogénea si los conjuntos son iguales:

${\displaystyle R(a_{1},a_{2}):\;(a_{1},a_{2})\in A_{1}\times A_{2}\land A_{1}=A_{2}}$

Dado que ${\displaystyle A_{1}}$ y ${\displaystyle A_{2}}$ son el mismo conjunto, se representa como:

${\displaystyle R(a_{1},a_{2}):\;(a_{1},a_{2})\in A\times A}$

O bien:

${\displaystyle R(a_{1},a_{2}):\;(a_{1},a_{2})\in A^{2}}$

Relación heterogénea

Una relación binaria R es heterogénea si los conjuntos no son iguales:

${\displaystyle R(a_{1},a_{2}):(a_{1},a_{2})\in A_{1}\times A_{2}\land A_{1}\neq A_{2}}$

Conceptos previos

Par ordenado

Dados los conjuntos ${\displaystyle A_{1}}$ y ${\displaystyle A_{2}}$ se describe el par ordenado ${\displaystyle (a_{1},a_{2})}$ que cumple:

${\displaystyle a_{1}\in A_{1}}$

${\displaystyle a_{2}\in A_{2}}$

Se representa como:

${\displaystyle A_{1}\times A_{2}=\{(a_{1},a_{2})\;:a_{1}\in A_{1}\land a_{2}\in A_{2}\}}$

Se lee como:

El producto cartesiano ${\displaystyle A_{1}\times A_{2}}$ es el subconjunto de los pares ordenados ${\displaystyle (a_{1},a_{2})}$ tal que ${\displaystyle a_{1}}$ pertenece a ${\displaystyle A_{1}}$ y ${\displaystyle a_{2}}$pertenece a ${\displaystyle A_{2}}$.

Producto cartesiano

${\displaystyle {\begin{array}{|r|ccc|}\hline a&(1,a)&(2,a)&(3,a)\\b&(1,b)&(2,b)&(3,b)\\c&(1,c)&(2,c)&(3,c)\\\hline A_{1}\times A_{2}&1&2&3\\\hline \end{array}}}$

Definidos los conjuntos:

${\displaystyle A_{1}=\{1,2,3\}}$

${\displaystyle A_{2}=\{a,b,c\}}$

El producto cartesiano ${\displaystyle A_{1}\times A_{2}}$ se describe en la tabla adjunta.

La relación binaria ${\displaystyle R(a_{1},a_{2})}$ queda definida como:

${\displaystyle A_{1}\times A_{2}=\{(1,a),(1,b),(1,c),(2,a),(2,b),(2,c),(3,a),(3,b),(3,c)\}\,}$

Relación binaria homogénea

Dado un único conjunto ${\displaystyle A=\{a,b,c,d\}}$, la relación binaria R queda determinada como:

${\displaystyle R\subset A^{2}}$

${\displaystyle R=\{(a,b),(b,c),(c,d),(d,d),(d,b),(b,a)\}}$

Una forma de representar el producto cartesiano es:

${\displaystyle R:A\rightarrow A}$

Tomando como conjunto inicial y final a ${\displaystyle A}$, se asocia un elemento inicial a uno final dentro de un mismo conjunto ${\displaystyle A}$, determinando una operación matemática, teniendo siempre en cuenta que si bien el conjunto inicial y final son el mismo, la relación es unidireccional. Si el elemento inicial está relacionado con el elemento final, necesariamente no implica que el elemento final esté relacionado con el elemento inicial.

En este caso el análisis de la relación binaria se hace según los distintos tipos de correspondencia con el mismo significado que en las relaciones heterogéneas

Representación de una relación binaria como subconjunto del producto cartesiano:

Dado el producto ${\displaystyle A\times A}$ de pares ordenados (x, y), donde x, y pertenecen a A, la relación binaria será el subconjunto de ${\displaystyle A\times A}$ que contiene todos los pares de elementos relacionados.

d	(a, d)	(b, d)	(c, d)	(d, d)
c	(a, c)	(b, c)	(c, c)	(d, c)
b	(a, b)	(b, b)	(c, b)	(d, b)
a	(a, a)	(b, a)	(c, a)	(d, a)
A×A	a	b	c	d

Si el producto ${\displaystyle A\times A}$ es:

${\displaystyle A\times A}$	${\displaystyle =\{\,}$	${\displaystyle (a,a),\,(a,b),\,(a,c),\,(a,d),}$
		${\displaystyle (b,a),\,(b,b),\,(b,c),\,(b,d),}$
		${\displaystyle (c,a),\,(c,b),\,(c,c),\,(c,d),}$
		${\displaystyle (d,a),\,(d,b),\,(d,c),\,(d,d)}$	${\displaystyle \}\,}$

el conjunto R de la relación binaria se representa:

${\displaystyle R=\{(a,b),(b,a),(b,c),(c,d),(d,b),(d,d)\}\,}$

Nótese que en el eje horizontal se representa el conjunto inicial, y en el eje vertical el conjunto final.

Propiedad de la relación binaria homogénea

Una relación binaria puede tener ciertas propiedades, según los pares ordenados que formen parte de dicha relación o no formen parte de ella, veamos algunas:

Propiedad reflexiva

Una relación tiene la propiedad reflexiva, si todo elemento está relacionado consigo mismo.

Si no todos los elementos del conjunto están relacionados consigo mismo se dice que la relación no es reflexiva o es arreflexiva.

${\displaystyle \forall a\in A:\;(a,a)\in R}$

Para todo elemento a que pertenezca al conjunto A, el par ordenado (a,a) pertenece a la relación binaria R.

Téngase en cuenta que debe cumplirse para todos los elementos del conjunto sin excepción, si esta propiedad solo se da en algunos casos la relación no es reflexiva:

${\displaystyle \nexists a\in A:\;(a,a)\notin R}$

No existe ningún elemento a en A, para el que el par ordenado (a,a) no pertenezca a la relación R. Puede verse que estas dos afirmaciones son iguales.

Propiedad irreflexiva

Una relación binaria tiene la propiedad irreflexiva, también llamada: antirreflexiva o antirrefleja, si ningún elemento del conjunto está relacionado consigo mismo:

${\displaystyle \forall a\in A:\;(a,a)\notin R}$

Que también puede expresarse

${\displaystyle \nexists a\in A:\;(a,a)\in R}$

No existe ningún elemento a en el conjunto A que cumpla que: (a,a) pertenezca a R.

Propiedad simétrica

Una relación binaria tiene la propiedad simétrica, si se cumple que un par ordenado (a,b) pertenece a la relación entonces el par (b,a) también pertenece a esa relación:

${\displaystyle \forall a,b\in A:\;(a,b)\in R\quad \longrightarrow \quad (b,a)\in R}$

Para todo par ordenado (a,b) que pertenezca a R, implica que el par (b,a) también pertenece a R, téngase en cuenta que si el par (a,b) no pertenece a la relación el par (b,a) tampoco tiene que pertenecer a esa relación:

${\displaystyle \nexists a,b\in A:\;(a,b)\in R\quad \land \quad (b,a)\notin R}$

No existe ningún par ordenado (a,b) que pertenezca a R y que el par (b,a) no pertenezca a R._[_

Propiedad antisimétrica

Una relación binaria se dice que tiene la propiedad antisimétrica si los pares ordenado (a,b) y (b,a) pertenecen a la relación entonces a = b:

${\displaystyle \forall a,b\in A:\;{\Big (}(a,b)\in R\quad \land \quad (b,a)\in R{\Big )}\quad \longrightarrow \quad a=b}$

Dicho de otra manera, no existen los elementos a, b de A, que cumplan las condiciones:

• a está relacionado con b
• b está relacionado con a
• a y b son distintos

${\displaystyle \nexists a,b\in A:\;(a,b)\in R\quad \land \quad (b,a)\in R\quad \land \quad a\neq b}$

Propiedad transitiva

Una relación binaria tiene la propiedad transitiva cuando, dado los elementos a, b, c del conjunto, si a está relacionado con b y b está relacionado con c, entonces a está relacionado con c:

${\displaystyle \forall a,b,c\in A:\;{\Big (}(a,b)\in R\quad \land \quad (b,c)\in R{\Big )}\quad \longrightarrow \quad (a,c)\in R}$

Propiedad intransitiva

Una relación binaria tiene la propiedad intransitiva cuando, dado los elementos a, b, c del conjunto, si a está relacionado con b y b está relacionado con c, entonces a no está relacionado con c:

${\displaystyle \forall a,b,c\in A:\;{\Big (}(a,b)\in R\quad \land \quad (b,c)\in R{\Big )}\quad \longrightarrow \quad (a,c)\notin R}$

Propiedad total

Una relación binaria se dice que es total: si para todo elemento del conjunto: a, b; o a está relacionado con b o b está relacionado con a, esto es el grafo de la relación es conexo:

${\displaystyle \forall a,b\in A:\;(a,b)\in R\quad \lor \quad (b,a)\in R}$

Clases de las relaciones binarias homogénea

Partiendo de las propiedades que una relación binaria homogéneas puede tener, se pueden diferenciar algunas por su especial interés:

Relación reflexiva

La propiedad reflexiva de una relación binaria es el inicio para los casos más elaborados, téngase en cuenta que las relaciones binarias no reflexivas y las irreflexivas son casos muy particulares muy poco estudiados, por su poca importancia en los casos más generales.

Las relaciones reflexivas son las definidas así:

Dado un conjunto A, y una relación binaria R entre sus elementos: ${\displaystyle R=\{(a,b)\in \;A^{2}:\quad R(a,b)\}}$ Se dice que R es relación reflexiva, si cumple: 1.- La propiedad reflexiva: ${\displaystyle \forall a\in A:\;(a,a)\in R}$ Todo elemento a de A está relacionado consigo mismo.

El caso más claro de propiedad reflexiva es la de igualdad matemática, así dado un conjunto de números, los naturales por ejemplo, y la propiedad de igualdad entre números, tenemos que todo número natural es igual a sí mismo.

Dado un conjunto A, formado por los siguientes elementos:

${\displaystyle A=\{a,b,c,d\}\;}$

Y una relación R entre los elementos del conjunto, definida así:

${\displaystyle \mathbb {R} ={\Big \{}(a,a),(a,b),(b,b),(b,c),(c,c),(d,b),(d,d){\Big \}}}$

Podemos ver que los pares ordenados que tienen sus dos términos iguales pertenecen a la relación:

${\displaystyle (a,a)\in \mathbb {R} \quad (b,b)\in \mathbb {R} \quad (c,c)\in \mathbb {R} \quad (d,d)\in \mathbb {R} }$

Luego la relación R es reflexiva.

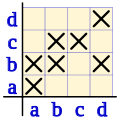
La relación R, también se puede representar en coordenadas cartesianas la función identidad.

En el eje horizontal (abscisas) representamos el conjunto inicial, de izquierda a derecha, y en el eje vertical(ordenadas) el conjunto final, de abajo arriba, si un determinado par pertenece a la relación se coloca una cruz en la casilla correspondiente, si no pertenece se deja en blanco, representando de este modo en coordenadas cartesianas la relación binaria.

En la diagonal principal, inferior izquierda, superior derecha, corresponde a los pares ordenados en los que sus dos elementos son iguales, si todas las casillas de esta diagonal tienen aspas, la relación es reflexiva.

Como puede verse en el diagrama, la relación estudiada es reflexiva, dado que:

Para todo elemento e del conjunto A, el par ordenado (e,e) pertenece a la relación R.

En cualquiera de las tres formas de representación vistas: enumeración de pares ordenados, donde los pares (e,e) pertenecen a la relación, el diagrama sagital, con una flecha que sale y llega a cada elemento del conjunto, o en coordenadas cartesianas, donde hay cruces en la diagonal principal, en todos los casos se representa una relación reflexiva, en la que todo elemento del conjunto está relacionado consigo mismo.

Relación no reflexiva

Los casos más estudiados de relaciones binarias homogéneas son las que cumplen la propiedad reflexiva, una relación que no cumple la propiedad reflexiva es no reflexiva, un caso particular de relación no reflexiva son las relaciones irreflexivas, en las que ningún elemento del conjunto está relacionado consigo mismo. Puede verse que si en una relación binaria algunos elementos están relacionados consigo mismo y otros no, la relación no es reflexiva y tampoco es irreflexiva, que se puede denominar arreflexiva. Ver diagrama:

${\displaystyle Relaciones\;homog{\acute {e}}neas{\begin{cases}reflexivas\\no\;reflexivas{\begin{cases}irreflexivas\\arreflexivas\end{cases}}\\\end{cases}}}$

Las relaciones irreflexivas son un caso particular de las no reflexivas.

Dado un conjunto A, y una relación binaria R entre sus elementos: ${\displaystyle R=\{(a,b)\in \;A^{2}:\quad R(a,b)\}}$ Se dice que R es relación irreflexiva, si cumple: 1.- La propiedad irreflexiva: ${\displaystyle \forall a\in A:\;(a,a)\notin R}$ Todo elemento a de A no está relacionado consigo mismo.

También podemos decir que una relación es irreflexiva si:

${\displaystyle \nexists a\in A\,:\quad (a,a)\in R}$

Una relación es irreflexiva si no existe un a en A que cumpla que a está relacionado consigo mismo.

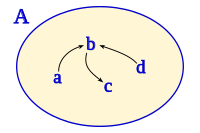
Dado el conjunto:

${\displaystyle A=\{a,b,c,d\}\,}$

y la relación entre los elementos de este conjunto:

${\displaystyle R={\Big \{}(a,b),(b,c),(d,b){\Big \}}}$

Podemos ver que:

${\displaystyle (a,a)\notin R\quad (b,b)\notin R\quad (c,c)\notin R\quad (d,d)\notin R}$

Para todo elemento e del conjunto A, el par ordenado (e,e) no pertenece a la relación R, luego esta relación en irreflexiva.

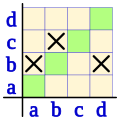
La representación de la relación en coordenadas cartesianas nos permite ver que la diagonal principal no tiene ninguna cruz, lo que es equivalente a la irrefrexibilidad de la relación.

La propiedad reflexiva e irreflexiva son mutuamente excluyentes en una misma relación, el cumplimiento de una de ellas da lugar al incumplimiento de la otra necesariamente, si una relación es reflexiva, tenemos que:

${\displaystyle \forall a\in A:\;(a,a)\in R}$

y si es irreflexiva, se cumple:

${\displaystyle \forall a\in A:\;(a,a)\notin R}$

Donde se ve claramente la incompatibilidad de las dos condiciones. El razonamiento contrario no es cierto dado que una relación binaria puede ser NO reflexiva y NO irreflexiva simultáneamente:

Una relación binaria es no reflexiva si:

${\displaystyle \exists a\in A\,:\quad (a,a)\notin R}$

Y una relación es no irreflexiva cuando:

${\displaystyle \exists a\in A\,:\quad (a,a)\in R}$

Estas dos condiciones son perfectamente compatibles, dando lugar a una relación binaria no reflexiva y no irreflexiva:

${\displaystyle {\begin{cases}\exists a\in A\,:\quad (a,a)\notin R\\\exists b\in A\,:\quad (b,b)\in R\end{cases}}}$

veamos un ejemplo, dado el conjunto:

${\displaystyle A=\{a,b,c,d\}\,}$

En la que se ha definido la relación binaria:

${\displaystyle R={\Big \{}(a,a),(a,b),(b,c),(c,c),(d,b){\Big \}}}$

Podemos ver que:

${\displaystyle (a,a)\in R\quad (c,c)\in R}$

Y también que:

${\displaystyle (b,b)\notin R\quad (d,d)\notin R}$

Luego la relación no es reflexiva y tampoco es irreflexiva.

Si representamos la relación binaria en coordenadas cartesianas, podemos ver que en la diagonal principal no todas las casillas tienen un aspa, luego la relación no es reflexiva, y tampoco están todas en blanco luego tampoco es irreflexiva, esto es un relación binaria no reflexiva y no irreflexiva, al darse estas dos condiciones simultáneamente en una misma relación.

En resumen, podemos diferenciar tres clases de relaciones:

• Relaciones reflexivas
• Relaciones irreflexivas
• Relaciones arreflexivas

Dado, que como ya se ha mencionado, una relación no puede ser reflexiva e irreflexiva simultáneamente, pero si puede ser no reflexiva y no irreflexiva simultáneamente.

Relación de dependencia

Una relación binaria es una relación de dependencia si es reflexiva y simétrica:

Dado un conjunto A, y una relación binaria R entre sus elementos: ${\displaystyle R=\{(a,b)\in \;A^{2}:\quad R(a,b)\}}$ Se dice que R es relación de dependencia, si cumple: 1.- La propiedad reflexiva: ${\displaystyle \forall a\in A:\;(a,a)\in R}$ Todo elemento a de A está relacionado consigo mismo. 2.- La propiedad simétrica: ${\displaystyle \forall a,b\in A:\;(a,b)\in R\quad \longrightarrow \quad (b,a)\in R}$ Si un elemento a está relacionado con otro b, entonces el b también está relacionado con el a.

Así por ejemplo si consideramos el conjunto de los números naturales, y definimos la distancia D entre dos números, como el valor absoluto de su diferencia:

${\displaystyle \forall a,b\in \mathbb {N} :\;D=|a-b|}$

y decimos que dos números naturales a, b están próximos si su distancia es a lo sumo un valor D conocido, tenemos que la relación binaria de proximidad es:

${\displaystyle (a,b)\in R:\;(a,b)\in \mathbb {N} ^{2}\quad \land \quad |a-b|\leq D}$

es una relación de dependencia, dado que es reflexiva:

${\displaystyle \forall a\in \mathbb {N} :\;|a-a|\leq D}$

es simétrica:

${\displaystyle \forall a,b\in \mathbb {N} :\;|a-b|\leq D\quad \longrightarrow \quad |b-a|\leq D}$

relación binaria de proximidad no es transitiva, dado que:

${\displaystyle \forall a,b,c\in \mathbb {N} :\;{\Big (}|a-b|\leq D\quad \land \quad |b-c|\leq D{\Big )}\quad \nrightarrow \quad |a-c|\leq D}$

que la distancia entre a y b sea a lo sumo D y que la distancia entre b y c no supere D, no implica necesariamente que la distancia entre a y c no sea mayor que D. Esta relación de dependencia entre los números por su distancia no es una clase de equivalencia, pero si denota una dependencia entre ellos.

Conjunto preordenado

Una relación binaria define un conjunto preordenado si es reflexiva y transitiva:

Dado un conjunto A, y una relación binaria R entre sus elementos: ${\displaystyle R=\{(a,b)\in \;A^{2}:\quad R(a,b)\}}$ Se dice que R define un conjunto preordenado, si cumple: 1.- La propiedad reflexiva: ${\displaystyle \forall a\in A:\;(a,a)\in R}$ Todo elemento a de A está relacionado consigo mismo. 2.- La propiedad transitiva: ${\displaystyle \forall a,b,c\in A:\;{\Big (}(a,b)\in R\quad \land \quad (b,c)\in R{\Big )}\longrightarrow \quad (a,c)\in R}$ Si un elemento a está relacionado con otro b, y este b con otro c, entonces el elemento a esta también relacionado con el c.

Relación de equivalencia

Una relación binaria es una relación de equivalencia si es reflexiva, simétrica y transitiva:^[1]​

Dado un conjunto A, y una relación binaria R entre sus elementos: ${\displaystyle R=\{(a,b)\in \;A^{2}:\quad R(a,b)\}}$ Se dice que R es relación de equivalencia, si cumple: 1.- La propiedad reflexiva: ${\displaystyle \forall a\in A:\;(a,a)\in R}$ Todo elemento a de A está relacionado consigo mismo. 2.- La propiedad simétrica: ${\displaystyle \forall a,b\in A:\;(a,b)\in R\longrightarrow \quad (b,a)\in R}$ Si un elemento a está relacionado con otro b, entonces el b también está relacionado con el a. 3.- La propiedad transitiva: ${\displaystyle \forall a,b,c\in A:\;{\Big (}(a,b)\in R\quad \land \quad (b,c)\in R{\Big )}\longrightarrow \quad (a,c)\in R}$ Si un elemento a está relacionado con otro b, y este b con otro c, entonces el elemento a esta también relacionado con el c.

Una relación de equivalencia define dentro del conjunto A lo que se denominan, Clases de equivalencia, una clase de equivalencia o familia de elementos es cada uno de los subconjuntos en que la relación de equivalencia divide al conjunto A, entre ellos son disjuntos, y la unión de todos ellos es el conjunto A, veamos un ejemplo.

En Aritmética modular se define la operación módulo como el resto de la división, así:

${\displaystyle 5{\mathit {\;M{\acute {o}}d\;}}2=1}$

${\displaystyle 6{\mathit {\;M{\acute {o}}d\;}}3=0}$

${\displaystyle 7{\mathit {\;M{\acute {o}}d\;}}3=1}$

el resto de dividir 5 entre 2 es 1

el resto de dividir 6 entre 3 es 0

el resto de dividir 7 entre 3 es 1

se dice que dos números son congruentes módulo n, si al dividir cada uno de esos números por n dan el mismo resto:

${\displaystyle 8\equiv 17\quad ({\mathit {M{\acute {o}}d\;}}3)}$

el 8 y el 17 son congruentes módulo 3 dado que al dividirlos por 3 en los dos casos dan por resto 2.

La congruencia modular de grado n, de los números naturales, es una Relación de equivalencia, dado que es reflexiva:

${\displaystyle \forall a\in \mathbb {N} :\;a\equiv a\quad ({\mathit {M{\acute {o}}d\;}}n)}$

es simétrica:

${\displaystyle \forall a,b\in \mathbb {N} :\;a\equiv b\quad ({\mathit {M{\acute {o}}d\;}}n)\longrightarrow \quad b\equiv a\quad ({\mathit {M{\acute {o}}d\;}}n)}$

y es transitiva

${\displaystyle \forall a,b,c\in \mathbb {N} :\;{\Big (}a\equiv b\quad ({\mathit {M{\acute {o}}d\;}}n)\quad \land \quad b\equiv c\quad ({\mathit {M{\acute {o}}d\;}}n){\Big )}\longrightarrow \quad a\equiv c\quad ({\mathit {M{\acute {o}}d\;}}n)}$

Conjunto parcialmente ordenado

Un conjunto A se dice que esta parcialmente ordenado respecto a una relación binaria R si la relación R es reflexiva, transitiva y antisimétrica:

Dado un conjunto A, y una relación binaria R entre sus elementos: ${\displaystyle R=\{(a,b)\in \;A^{2}:\quad R(a,b)\}}$ Se dice que R define un conjunto parcialmente ordenado, si cumple: 1.- La propiedad reflexiva: ${\displaystyle \forall a\in A:\;(a,a)\in R}$ Todo elemento a de A está relacionado consigo mismo. 2.- La propiedad transitiva: ${\displaystyle \forall a,b,c\in A:\;{\Big (}(a,b)\in R\quad \land \quad (b,c)\in R{\Big )}\longrightarrow \quad (a,c)\in R}$ Si un elemento a está relacionado con otro b, y este b con otro c, entonces el elemento a esta también relacionado con el c. 3.- La propiedad antisimétrica: ${\displaystyle \forall a,b\in A:\;{\Big (}(a,b)\in R\quad \land \quad (b,a)\in R{\Big )}\longrightarrow \quad a=b}$ Si los pares ordenado (a,b) y (b,a) pertenecen a la relación R, entonces a y b son iguales.

Tomando un conjunto A, formado, por ejemplo, por los elementos:

${\displaystyle A=\{a,b,c\}\;}$

Se define el Conjunto potencia de A como el formado por todos los subconjuntos de A:

${\displaystyle P(A)={\Big \{}\{\},\{a\},\{b\},\{c\},\{a,b\},\{a,c\},\{b,c\},\{a,b,c\}{\Big \}}}$

A cada uno de estos subconjuntos los llamamos:

${\displaystyle A_{1}=\{\}\;}$

${\displaystyle A_{2}=\{a\}\;}$

${\displaystyle A_{3}=\{b\}\;}$

${\displaystyle A_{4}=\{c\}\;}$

${\displaystyle A_{5}=\{a,b\}\;}$

${\displaystyle A_{6}=\{a,c\}\;}$

${\displaystyle A_{7}=\{b,c\}\;}$

${\displaystyle A_{8}=\{a,b,c\}\;}$

Y tomando dos de estos subconjuntos decimos que están relacionados por pertenencia si el primero es Subconjunto del segundo:

${\displaystyle R={\Big \{}(A_{i},A_{j})\in \;P(A):\quad A_{i}\subseteq A_{j}{\Big \}}}$

La relación pertenencia entre los conjuntos potencia de A, es un conjunto parcialmente ordenado, al ser reflexiva:

${\displaystyle \forall A_{i}\in P(A):\;A_{i}\subseteq A_{i}}$

Transitiva:

${\displaystyle \forall A_{i},A_{j},A_{k}\in P(A):\;{\Big (}A_{i}\subseteq A_{j}\quad \land \quad A_{j}\subseteq A_{k}{\Big )}\longrightarrow \quad A_{i}\subseteq A_{k}}$

Antisimetrica:

${\displaystyle \forall A_{i},A_{j}\in P(A):\;{\Big (}A_{i}\subseteq A_{j}\quad \land \quad A_{j}\subseteq A_{i}{\Big )}\longrightarrow \quad A_{i}=A_{j}}$

Por lo que el conjunto de las partes de A, respecto a la relación binaria pertenencia es un conjunto parcialmente ordenado.

Esta relación no es total dado que:

${\displaystyle \neg \forall (A_{i},A_{j})\in P(A):\;A_{i}\subseteq A_{j}\quad \lor \quad A_{j}\subseteq A_{i}}$

Que se denominan no comparables, los pares de conjuntos no comparables son:

${\displaystyle 1.\;{\Big (}\{a\},\{b\}{\Big )}\notin R\;:\quad \{a\}\nsubseteq \{b\}\;\land \;\{b\}\nsubseteq \{a\}}$

${\displaystyle 2.\;{\Big (}\{a\},\{c\}{\Big )}\notin R\;:\quad \{a\}\nsubseteq \{c\}\;\land \;\{c\}\nsubseteq \{a\}}$

${\displaystyle 3.\;{\Big (}\{b\},\{c\}{\Big )}\notin R\;:\quad \{b\}\nsubseteq \{c\}\;\land \;\{c\}\nsubseteq \{b\}}$

${\displaystyle 4.\;{\Big (}\{a\},\{b,c\}{\Big )}\notin R\;:\quad \{a\}\nsubseteq \{b,c\}\;\land \;\{b,c\}\nsubseteq \{a\}}$

${\displaystyle 5.\;{\Big (}\{b\},\{a,c\}{\Big )}\notin R\;:\quad \{b\}\nsubseteq \{a,c\}\;\land \;\{a,c\}\nsubseteq \{b\}}$

${\displaystyle 6.\;{\Big (}\{c\},\{a,b\}{\Big )}\notin R\;:\quad \{c\}\nsubseteq \{a,b\}\;\land \;\{a,b\}\nsubseteq \{c\}}$

${\displaystyle 7.\;{\Big (}\{a,b\},\{a,c\}{\Big )}\notin R\;:\quad \{a,b\}\nsubseteq \{a,c\}\;\land \;\{a,c\}\nsubseteq \{a,b\}}$

${\displaystyle 8.\;{\Big (}\{a,b\},\{b,c\}{\Big )}\notin R\;:\quad \{a,b\}\nsubseteq \{b,c\}\;\land \;\{b,c\}\nsubseteq \{a,b\}}$

${\displaystyle 9.\;{\Big (}\{a,c\},\{b,c\}{\Big )}\notin R\;:\quad \{a,c\}\nsubseteq \{b,c\}\;\land \;\{b,c\}\nsubseteq \{a,c\}}$

A la vista del diagrama, los conjuntos que se pueden alcanzar siguiendo el sentido de las flechas se denominan comparables y determinan la estructura del orden parcial.

Conjunto acotado

Para un conjunto A y una relación binaria ${\displaystyle \precsim }$ definida entre los elementos de A, que expresaremos ${\displaystyle (A,\precsim )}$ y la relación la representamos:

${\displaystyle x,y\in A\;,\quad x\precsim y}$

que se lee: x antecede a y.

La no relación se representa:

${\displaystyle x,y\in A\;,\quad x\not \precsim y}$

Todo elemento a de A está relacionado consigo mismo.

2.- La relación R es transitiva:

${\displaystyle \forall a,b,c\in A:\;{\Big (}(a,b)\in R\quad \land \quad (b,c)\in R{\Big )}\longrightarrow \quad (a,c)\in R}$

Si un elemento a está relacionado con otro b, y este b con otro c, entonces el elemento a esta también relacionado con el c.

3.- La relación R es antisimétrica:

${\displaystyle \forall a,b\in A:\;{\Big (}(a,b)\in R\quad \land \quad (b,a)\in R{\Big )}\longrightarrow \quad a=b}$

Si los pares ordenado (a,b) y (b,a) pertenecen a la relación R, entonces a y b son iguales.

4.- La relación R es total:

${\displaystyle \forall a,b\in A:\;(a,b)\in R\quad \lor \quad (b,a)\in R}$

Si para cualquiera dos elemento del conjunto: a, b; o a está relacionado con b o bien b está relacionado con a.

Si tomamos el conjunto de los números enteros Z, por ejemplo, respecto a la relación binaria entre sus elementos menor o igual, podemos ver que es reflexiva:

${\displaystyle \forall a\in \mathbb {Z} :\;a\leq a}$

es transitiva:

${\displaystyle \forall a,b,c\in \mathbb {Z} :\;{\Big (}a\leq b\quad \land \quad b\leq c{\Big )}\longrightarrow \quad a\leq c}$

es antisimetrica:

${\displaystyle \forall a,b\in \mathbb {Z} :\;{\Big (}a\leq b\quad \land \quad b\leq a{\Big )}\longrightarrow \quad a=b}$

y es total:

${\displaystyle \forall a,b\in \mathbb {Z} :\;a\leq b\quad \lor \quad b\leq a}$

Conjunto con orden total y acotado

Dado un conjunto A y una relación binaria ${\displaystyle \precsim }$ definida entre los elementos de A, que expresaremos ${\displaystyle (A,\precsim )}$ y la relación se representa:

${\displaystyle a\precsim b}$

Se dice que se ha definido un orden total en el conjunto A, si la relación ${\displaystyle (A,\precsim )}$ cumple las propiedades:

1. Reflexiva.

2. Antisimétrica.

3. Transitiva.

4. Es, además, una relación total, es decir, se cumple que todos los elementos de un conjunto con orden total son comparables:

${\displaystyle \forall a,b\in A:\quad a\precsim b\quad \lor \quad b\precsim a}$

Dado un conjunto A en el que se ha definido una relación binaria ${\displaystyle \precsim }$, siendo ${\displaystyle (A,\precsim )}$ un conjunto totalmente ordenado.

El elemento y de A que cumple:

${\displaystyle y\in A\;es\;m{\acute {a}}ximo\;si:\quad \forall x\in A\;/\quad x\precsim y}$

Se denomina máximo y define una cota superior en A; el elemento máximo es único. Si el conjunto A y la relación binaria ${\displaystyle \precsim }$, que expresaremos ${\displaystyle (A,\precsim )}$ es un orden total y tiene máximo, entonces es un conjunto con orden total y acotado superiormente.

Del mismo modo el elemento z de A que cumple:

${\displaystyle z\in A\;es\;m{\acute {\imath }}nimo\;si:\quad \forall x\in A\;/\quad z\precsim x}$

Se denomina mínimo y define una cota inferior en A; el elemento mínimo es único. Si el conjunto A y la relación binaria ${\displaystyle \precsim }$, que expresaremos ${\displaystyle (A,\precsim )}$ es un orden total y tiene mínimo, entonces es un conjunto con orden total y acotado inferiormente.

Un conjunto con orden total solo se dice acotado, si está acotado superior e inferiormente.

Relación binaria heterogénea

Una relación binaria entre dos conjuntos A y B, se llama heterogénea cuando A es distinto de B:

${\displaystyle R(a,b):\;(a,b)\in A\times B\quad \land \quad A\neq B}$

Lo que también se llama correspondencia matemática.^[2]​^[3]​

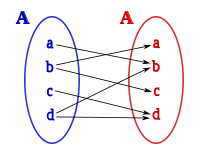
A la derecha podemos ver lo que se denomina un diagrama sagital, en el cual se representan los dos conjuntos de la relación binaria, asociando los elementos de uno y otro conjunto con una flecha, que sale del elemento origen y llega al elemento imagen, en el diagrama pueden verse un conjunto de pinceles con pintura de color y un conjunto de caras pintadas, asociando a cada pincel la cara que está pintada del mismo color.

Puede haber pinceles o caras del mismo color, pero deben ser considerados como elementos distintos del conjunto, si dos pinceles o dos caras son del mismo color tienen la misma característica color, siendo elementos del conjunto diferentes.

En el diagrama podemos ver el conjunto inicial ( o dominio ) de pinceles P, sobre el que está definida la relación:

${\displaystyle P=\{\,}$

,

,

,

${\displaystyle \}\,}$

Solo algunos elementos del conjunto inicial tienen asociado un elemento, estos elementos forman el conjunto origen:

${\displaystyle O=\{\,}$

,

,

${\displaystyle \}\,}$

Y el conjunto final ( o codominio ) de caras pintadas C es:

${\displaystyle C=\{\,}$

,

,

,

${\displaystyle \}\,}$

Los elementos del conjunto final a los que se les ha asociado un origen se llama conjunto imagen:

${\displaystyle I=\{\,}$

,

,

${\displaystyle \}\,}$

La relación binaria es la formada por los pares ordenados:

${\displaystyle R=\,\{(}$

,

${\displaystyle ),\,(}$

,

${\displaystyle ),\,(}$

,

${\displaystyle ),\,(}$

,

${\displaystyle )\}\,}$

Una relación binaria homogénea:

${\displaystyle R(a,b):\;(a,b)\in A\times A}$

Puede ser tratada como heterogénea considerando el conjunto inicial y final como distintos, si lo que se está tratando es una correspondencia, con la misma validez que si los conjuntos serían distintos, pudiendo realizar simultáneamente su análisis como relación homogénea, si es factible.

Propiedades de las relaciones binarias heterogénea

Partiendo de una relación binarias heterogénea R, entre los conjunto A y B:

${\displaystyle R:A\rightarrow B}$

Por su importancia podemos distinguir las siguientes condiciones, que nos permiten diferenciar los subtipos de correspondencias.

Condición de existencia de imagen. (ei)

La condición de existencia de imagen garantiza que tomando un elemento cualesquiera a de A tiene al menos una imagen b en B.

${\displaystyle \forall a\in A:\;\exists b\in B\quad \land \quad (a,b)\in R.}$

para todo elemento a de A se cumple que existe al menos un b de B, a y b estén relacionado.

En la figura podemos ver el conjunto P de los pinceles:

${\displaystyle P=\{\,}$

,

${\displaystyle \}\,}$

y el C de las caras pintada:

${\displaystyle C=\{\,}$

,

,

,

${\displaystyle \}\,}$

Si relacionamos cada pincel con la cara pintada del mismo color, podemos ver que todos los pinceles tienen al menos una cara asociada.

Condición de existencia de origen. (eo)

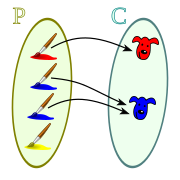
La condición de existencia de origen garantiza que todo elemento b de B tiene al menos un origen a en A.

${\displaystyle \forall b\in B:\;\exists a\in A\quad \land \quad (a,b)\in R.}$

para todo b de B se cumple que existe un a en A y que a y b están relacionados.

Si vemos la figura podemos ver el conjunto P de pinceles con pintura:

${\displaystyle P=\{\,}$

,

,

,

${\displaystyle \}\,}$

y el conjunto C de caras pintada:

${\displaystyle C=\{\,}$

,

${\displaystyle \}\,}$

Y que todas y cada una de las caras tiene al menos un pincel de su mismo color. Cada uno de los elementos del conjunto final tiene un origen.

Condición de unicidad de imagen. (ui)

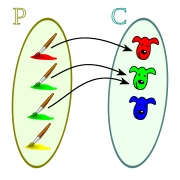
La condición de unicidad de imagen garantiza que los elementos a de A que están relacionados con algún b de B está relacionado con un único elemento b de B, es decir:

${\displaystyle {\Big (}(a,b_{1})\in R\quad \land \quad (a,b_{2})\in R{\Big )}\longrightarrow \quad b_{1}=b_{2}.}$

si un elemento a de A está relacionado con dos elementos b de B esos dos elementos son iguales.

Condición de unicidad de imagen garantiza que los elementos que tienen imagen tengan una sola imagen, pero no garantiza que todos los elementos de A tengan imagen, esta diferencia es importante.

En el diagrama sagital de la derecha vemos el conjunto P:

${\displaystyle P=\{\,}$

,

,

,

${\displaystyle \}\,}$

Y el conjunto final C, de caras pintada:

${\displaystyle C=\{\,}$

,

,

${\displaystyle \}\,}$

Los pinceles que tienen una cara relacionada, tienen una sola cara relacionada.

Condición de unicidad de origen. (uo)

La condición de unicidad de origen dice: que los elementos b de B que están relacionados con algún a de A está relacionado solo con un único elemento a de A, es decir:

${\displaystyle {\Big (}(a_{1},b)\in R\quad \land \quad (a_{2},b)\in R{\Big )}\longrightarrow \quad a_{1}=a_{2}.}$

En el diagrama tenemos el conjunto inicial P de pinceles con pintura de colores:

${\displaystyle P=\{\,}$

,

,

,

${\displaystyle \}\,}$

y el conjunto final C de caras pintadas:

${\displaystyle C=\{\,}$

,

,

,

${\displaystyle \}\,}$

Relacionando cada pincel con la cara de su mismo color, podemos ver que las caras que tienen un pincel relacionado, solo tienen un pincel relacionado, esto es un solo origen, no todas las caras tienen un origen, pero las que lo tienen, tienen un solo origen.

Galería de ejemplos

Según las cuatro condiciones expuestas, cada una de ellas independiente de las demás, podemos ver una serie de ejemplos ilustrativos de los casos que se pueden presentar.

Utilizaremos como conjunto inicial el conjunto de tubos de pintura T, y como conjunto final el de pinceles P, asociando cada tubo de pintura con el pincel del mismo color.

Correspondencia Existencia imagen: no Unicidad imagen: no Existencia origen: no Unicidad origen: no	Correspondencia Existencia imagen: si Unicidad imagen: no Existencia origen: no Unicidad origen: no	C. Unívoca Existencia imagen: no Unicidad imagen: si Existencia origen: no Unicidad origen: no	Aplicación Existencia imagen: si Unicidad imagen: si Existencia origen: no Unicidad origen: no
Correspondencia Existencia imagen: no Unicidad imagen: no Existencia origen: si Unicidad origen: no	Correspondencia Existencia imagen: si Unicidad imagen: no Existencia origen: si Unicidad origen: no	C. Unívoca Existencia imagen: no Unicidad imagen: si Existencia origen: si Unicidad origen: no	A. Sobreyectiva Existencia imagen: si Unicidad imagen: si Existencia origen: si Unicidad origen: no
Correspondencia Existencia imagen: no Unicidad imagen: no Existencia origen: no Unicidad origen: si	Correspondencia Existencia imagen: si Unicidad imagen: no Existencia origen: no Unicidad origen: si	C. Biunívoca Existencia imagen: no Unicidad imagen: si Existencia origen: no Unicidad origen: si	A. Inyectiva Existencia imagen: si Unicidad imagen: si Existencia origen: no Unicidad origen: si
Correspondencia Existencia imagen: no Unicidad imagen: no Existencia origen: si Unicidad origen: si	Correspondencia Existencia imagen: si Unicidad imagen: no Existencia origen: si Unicidad origen: si	C. Biunívoca Existencia imagen: no Unicidad imagen: si Existencia origen: si Unicidad origen: si	A. Biyectiva Existencia imagen: si Unicidad imagen: si Existencia origen: si Unicidad origen: si

Clases de las relaciones binarias heterogénea

Partiendo de las características de las relaciones binarias heterogéneas, podemos diferenciar los siguientes casos.

Correspondencia unívoca

Una correspondencia es unívoca si cumple la condición de unicidad de imagen:

Dada una relación binarias heterogénea R, entre los conjunto A y B: ${\displaystyle R:A\rightarrow B}$ Esta relación es una correspondencia unívoca, si cumple: 1.- Unicidad de imagen: se dice que cumple la condición de unicidad de imagen si los elementos a de A que tienen imagen, tienen una sola imagen: ${\displaystyle {\Big (}(a,b_{1})\in R\quad \land \quad (a,b_{2})\in R{\Big )}\quad \longrightarrow \quad b_{1}=b_{2}.}$

Esta condición en necesaria y suficiente para que una correspondencia sea considerada unívoca.

Correspondencia biunívoca

Una correspondencia es biunívoca si cumple las condiciones de unicidad de imagen y unicidad de origen:

Dada una relación binarias heterogénea R, entre los conjunto A y B: ${\displaystyle R:A\rightarrow B}$ Esta relación es una correspondencia biunívoca, si cumple: 1.- Unicidad de imagen: se dice que cumple la condición de unicidad de imagen si los elementos a de A que tienen imagen, tienen una sola imagen: ${\displaystyle {\Big (}(a,b_{1})\in R\quad \land \quad (a,b_{2})\in R{\Big )}\quad \longrightarrow \quad b_{1}=b_{2}.}$ 2.- Unicidad de origen: se dice que cumple la condición de unicidad de origen si los elementos b de B que tienen origen, tienen un solo origen: ${\displaystyle {\Big (}(a_{1},b)\in R\quad \land \quad (a_{2},b)\in R{\Big )}\quad \longrightarrow \quad a_{1}=a_{2}.}$

Aplicación

Una correspondencia ${\displaystyle R:A\to B}$ se denomina aplicación si todo elemento de A admite una única imagen en B.,^[4]​^[5]​^[3]​^[6]​^[7]​^[8]​ esto es si cumple la condición de unicidad de imagen y de existencia de imagen.

Una aplicación f de A en B, siendo A y B dos conjuntos cualesquiera, es una correspondencia entre A y B, total y unívoca.^[9]​ según otra nomenclatura.

Si la aplicación la representamos como R, tendremos:

${\displaystyle {\begin{array}{rcl}R:\;A&\longrightarrow &B\\a&\longmapsto &b=R(a)\end{array}}}$

por la que definimos una aplicación que a cada elemento a de A se le asigna un único b de B.

${\displaystyle \forall a\in A\,:\quad \exists !b\in B\;/\quad b=R(a)}$

Para todo a de A, se cumple que existe un único b de B, tal que b es el resultado R(a).

El término función se suele utilizar cuando los conjuntos inicial y final son numéricos.^[10]​

Es usual hablar de aplicación en lugar de función, reservando esta última expresión, habitualmente, para el caso en el cual los conjuntos A y B son numéricos. Si A y B son conjuntos de puntos, se suele hablar de transformación geométrica.^[11]​

Una función es el término usado para indicar la relación o correspondencia entre dos o más cantidades.^[12]​

En inglés una aplicación se llama map^[13]​

Dada una relación binarias heterogénea R, entre los conjunto A y B: ${\displaystyle R:A\rightarrow B}$ Esta relación es una aplicación, si cumple: 1.- Unicidad de imagen: se dice que cumple la condición de unicidad de imagen si los elementos a de A que tienen imagen, tienen una sola imagen: ${\displaystyle {\Big (}(a,b_{1})\in R\quad \land \quad (a,b_{2})\in R{\Big )}\quad \longrightarrow \quad b_{1}=b_{2}.}$ 2.- Existencia de imagen: se dice que cumple la condición de existencia de imagen si para todos los elementos a de A existe al menos una imagen b en B: ${\displaystyle \forall a\in A:\;\exists b\in B\quad \land \quad (a,b)\in R.}$

Si una correspondencia cumple estas dos condiciones se denomina aplicación.

Aplicación inyectiva

Una correspondencia es una aplicación inyectiva si cumple la condición de unicidad de imagen, existencia de imagen y unicidad de origen.

Dada una relación binarias heterogénea R, entre los conjunto A y B: ${\displaystyle R:A\rightarrow B}$ Esta relación es una aplicación inyectiva, si cumple: 1.- Unicidad de imagen: se dice que cumple la condición de unicidad de imagen si los elementos a de A que tienen imagen, tienen una sola imagen: ${\displaystyle {\Big (}(a,b_{1})\in R\quad \land \quad (a,b_{2})\in R{\Big )}\quad \longrightarrow \quad b_{1}=b_{2}.}$ 2.- Existencia de imagen: se dice que cumple la condición de existencia de imagen si para todos los elementos a de A existe al menos una imagen b en B: ${\displaystyle \forall a\in A:\;\exists b\in B\quad \land \quad (a,b)\in R.}$ 3.- Unicidad de origen: se dice que cumple la condición de unicidad de origen si los elementos b de B que tienen origen, tienen un solo origen: ${\displaystyle {\Big (}(a_{1},b)\in R\quad \land \quad (a_{2},b)\in R{\Big )}\quad \longrightarrow \quad a_{1}=a_{2}.}$

Como puede verse una aplicación que cumple la condición de unicidad de origen es una Aplicación inyectiva.

De otra forma no tan usual, podemos decir que una correspondencia biunívoca que cumpla la condición de existencia de imagen también es una aplicación inyectiva.

Aplicación sobreyectiva

Una correspondencia se llama Aplicación sobreyectiva si cumple la condición de unicidad de imagen, existencia de imagen y existencia de origen:

Dada una relación binarias heterogénea R, entre los conjunto A y B: ${\displaystyle R:A\rightarrow B}$ Esta relación es una aplicación sobreyectiva, si cumple: 1.- Unicidad de imagen: se dice que cumple la condición de unicidad de imagen si los elementos a de A que tienen imagen, tienen una sola imagen: ${\displaystyle {\Big (}(a,b_{1})\in R\quad \land \quad (a,b_{2})\in R{\Big )}\quad \longrightarrow \quad b_{1}=b_{2}.}$ 2.- Existencia de imagen: se dice que cumple la condición de existencia de imagen si para todos los elementos a de A existe al menos una imagen b en B: ${\displaystyle \forall a\in A:\;\exists b\in B\quad \land \quad (a,b)\in R.}$ 3.- Existencia de origen: se dice que cumple la condición de existencia de origen si para todos los elementos b de B existe al menos un origen a en A: ${\displaystyle \forall b\in B:\;\exists a\in A\quad \land \quad (a,b)\in R.}$

Se puede decir que una aplicación sobreyectiva, es una aplicación que cumple la condición de existencia de origen.

Aplicación biyectiva

Una correspondencia es una aplicación biyectiva si cumple las condiciones de unicidad de imagen, existencia de imagen, unicidad de origen y existencia de origen:

Dada una relación binarias heterogénea R, entre los conjunto A y B: ${\displaystyle R:A\rightarrow B}$ Esta relación es una aplicación biyectiva, si cumple: 1.- Unicidad de imagen: se dice que cumple la condición de unicidad de imagen si los elementos a de A que tienen imagen, tienen una sola imagen: ${\displaystyle {\Big (}(a,b_{1})\in R\quad \land \quad (a,b_{2})\in R{\Big )}\quad \longrightarrow \quad b_{1}=b_{2}.}$ 2.- Existencia de imagen: se dice que cumple la condición de existencia de imagen si para todos los elementos a de A existe al menos una imagen b en B: ${\displaystyle \forall a\in A:\;\exists b\in B\quad \land \quad (a,b)\in R.}$ 3.- Unicidad de origen: se dice que cumple la condición de unicidad de origen si los elementos b de B que tienen origen, tienen un solo origen: ${\displaystyle {\Big (}(a_{1},b)\in R\quad \land \quad (a_{2},b)\in R{\Big )}\quad \longrightarrow \quad a_{1}=a_{2}.}$ 4.- Existencia de origen: se dice que cumple la condición de existencia de origen si para todos los elementos b de B existe al menos un origen a en A: ${\displaystyle \forall b\in B:\;\exists a\in A\quad \land \quad (a,b)\in R.}$

Una Aplicación es biyectiva, si es inyectiva y sobreyectiva.

Propiedades

Las relaciones binarias pueden tener o no estas propiedades. R será:

Relación reflexiva	${\displaystyle \forall a\in A,\;(a,a)\in R}$
Relación irreflexiva	${\displaystyle \forall a\in A,\;(a,a)\notin R}$
Relación simétrica	${\displaystyle \forall a,b\in A,\;(a,b)\in R\Rightarrow (b,a)\in R}$
Relación asimétrica	${\displaystyle \forall a,b\in A,\;(a,b)\in R\Rightarrow (b,a)\notin R}$
Relación antisimétrica	${\displaystyle \forall a,b\in A,\;(a,b)\in R\;\land \;(b,a)\in R\Rightarrow a=b}$
Relación transitiva	${\displaystyle \forall a,b,c\in A,\;(a,b)\in R\;\land \;(b,c)\in R\Rightarrow (a,c)\in R}$
Relación intransitiva	${\displaystyle \forall a,b,c\in A,\;(a,b)\in R\;\land \;(b,c)\in R\Rightarrow (a,c)\notin R}$
Relación circular	${\displaystyle \forall a,b,c\in A,\;(a,b)\in R\;\land \;(b,c)\in R\Rightarrow (c,a)\in R}$
Relación total	${\displaystyle \forall a,b\in A,\;(a,b)\in R\;\lor \;(b,a)\in R}$

Véase también

• Teoría del orden

Referencias

Bibliografía

1. González Gómez, Antonia (6 de 2009). Álgebra lineal. Fundación Conde del Valle de Salazar. ISBN 978-84-96442-28-3.  La referencia utiliza el parámetro obsoleto |mes= (ayuda)
2. Baquerizo Azofra, Clara (4 de 2008). Matemática discreta y álgebra lineal (1 edición). Martín Gómez, Emilia. ISBN 978-84-612-3787-6.  La referencia utiliza el parámetro obsoleto |mes= (ayuda)
3. Hortalá González, María Teresa (10 de 2001). Matemática discreta y lógica matemática (2 edición). Editorial Complutense, S.A. ISBN 978-84-7491-650-8.  La referencia utiliza el parámetro obsoleto |mes= (ayuda)
4. Climent Coloma, Joan Josep (6 de 2001). Álgebra. Teoría de conjuntos y estructuras algebraicas (1 edición). Editorial Club Universitario. ISBN 978-84-8454-081-6.  La referencia utiliza el parámetro obsoleto |mes= (ayuda)
5. Gutiérrez Gómez, Andrés; García Castro, Fernando (1981). Álgebra lineal (1 edición). Ediciones Pirámide, S.A. ISBN 978-84-368-0174-3.  La referencia utiliza el parámetro obsoleto |coautores= (ayuda)
6. Losada Rodríguez, Ramón (7 de 1978). Análisis matemático. Ediciones Pirámide, S.A. ISBN 978-84-368-0096-8.  La referencia utiliza el parámetro obsoleto |mes= (ayuda)
7. Losada Rodríguez, Ramón (9 de 1973). Conjuntos Álgebra Lineal (2 edición). ISBN 978-84-400-6592-6.  La referencia utiliza el parámetro obsoleto |mes= (ayuda)

Enlaces externos

• Relaciones binarias
• Relaciones binarias
• Conjuntos, aplicaciones y relaciones binarias.
• Relaciones binarias y grafos
• Relación (enlace roto disponible en Internet Archive; véase el historial, la primera versión y la última).
• Introducción a las estructuras algebraicas