Stable ∞-category

In category theory, a branch of mathematics, a stable ∞-category is an ∞-category such that^[1]

• (i) It has a zero object.
• (ii) Every morphism in it admits a fiber and cofiber.
• (iii) A triangle in it is a fiber sequence if and only if it is a cofiber sequence.

The homotopy category of a stable ∞-category is triangulated.^[2] A stable ∞-category admits finite limits and colimits.^[3]

Examples: the derived category of an abelian category and the ∞-category of spectra are both stable.

A stabilization of an ∞-category C having finite limits and base point is a functor from the stable ∞-category S to C. It preserves limit. The objects in the image have the structure of infinite loop spaces; whence, the notion is a generalization of the corresponding notion (stabilization (topology)) in classical algebraic topology.

By definition, the t-structure of a stable ∞-category is the t-structure of its homotopy category. Let C be a stable ∞-category with a t-structure. Then every filtered object ${\displaystyle X(i),i\in \mathbb {Z} }$ in C gives rise to a spectral sequence ${\displaystyle E_{r}^{p,q}}$, which, under some conditions, converges to ${\displaystyle \pi _{p+q}\operatorname {colim} X(i).}$^[4] By the Dold–Kan correspondence, this generalizes the construction of the spectral sequence associated to a filtered chain complex of abelian groups.

Notes

References

• Lurie, J. "Higher Algebra" (PDF). last updated August 2017

• v
• t
• e

Category theory

Key concepts

Key concepts Category Abelian Additive Concrete Pre-abelian Preadditive Bicategory Adjoint functors CCC Commutative diagram End Exponential Functor Kan extension Morphism Natural transformation Universal property Universal constructions Limits Terminal objects Products Equalizers Kernels Pullbacks Inverse limit Colimits Initial objects Coproducts Coequalizers Cokernels and quotients Pushout Direct limit Algebraic categories Sets Relations Magmas Groups Abelian groups Rings (Fields) Modules (Vector spaces) Constructions on categories Free category Functor category Kleisli category Opposite category Quotient category Product category Comma category Subcategory

Higher category theory

Key concepts Categorification Enriched category Higher-dimensional algebra Homotopy hypothesis Model category Simplex category String diagram Topos n-categories Weak n-categories Bicategory (pseudofunctor) Tricategory Tetracategory Kan complex ∞-groupoid ∞-topos Strict n-categories 2-category (2-functor) 3-category Categorified concepts 2-group 2-ring En-ring (Traced)(Symmetric) monoidal category n-group n-monoid

• Category
• Outline
• Glossary

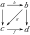This category theory-related article is a stub. You can help Wikipedia by expanding it.

• v
• t
• e