Convergència (sèries)

Aquest article o secció no cita les fonts o necessita més referències per a la seva verificabilitat.

En matemàtiques, una sèrie és la suma dels termes d'una successió infinita de nombres.

Donada una seqüència infinita ${\displaystyle \left(a_{1},\ a_{2},\ a_{3},\dots \right)}$, l'enèssima suma parcial ${\displaystyle S_{n}}$ és la suma dels primers n termes de la seqüència, és a dir:

${\displaystyle S_{n}=\sum _{k=1}^{n}a_{k}.}$

Una sèrie és convergent si la seqüència de les seves sumes parcials ${\displaystyle \left\{S_{1},\ S_{2},\ S_{3},\dots \right\}}$ tendeix a un límit; és a dir que les sumes parcials s'acosten més i més a un determinat nombre quan el nombre de termes augmenta. Més precisament, una sèrie convergeix si existeix un nombre ${\displaystyle \ell }$ tal que per qualsevol nombre positiu petit i arbitrari ${\displaystyle \varepsilon }$, existeix un enter suficientment gran ${\displaystyle N}$ tal que per tot ${\displaystyle n\geq \ N}$,

${\displaystyle \left|S_{n}-\ell \right\vert \leq \ \varepsilon .}$

Si la sèries és convergent, el nombre ${\displaystyle \ell }$ (necessàriament únic) s'anomena 'suma de la sèrie.

Qualsevol sèrie no convergent s'anomena sèrie divergent.

Exemples i contraexemples

• Els inversos dels nombres naturals formen una sèrie divergent (sèrie harmònica):
• : ${\displaystyle {1 \over 1}+{1 \over 2}+{1 \over 3}+{1 \over 4}+{1 \over 5}+{1 \over 6}+\cdots \rightarrow \infty .}$
• Alternant el signes dels inversos del nombres naturals es produeix, en canvi, una sèrie que convergeix al logaritme natural de 2:
• : ${\displaystyle {1 \over 1}-{1 \over 2}+{1 \over 3}-{1 \over 4}+{1 \over 5}\cdots =\ln(2)}$
• Els inversos dels nombres primers formen una sèrie divergent:
• : ${\displaystyle {1 \over 2}+{1 \over 3}+{1 \over 5}+{1 \over 7}+{1 \over 11}+{1 \over 13}+\cdots \rightarrow \infty .}$
• Els inversos dels nombres triangulars pridueix la sèrie convergent:
• : ${\displaystyle {1 \over 1}+{1 \over 3}+{1 \over 6}+{1 \over 10}+{1 \over 15}+{1 \over 21}+\cdots =2.}$
• Els inversos dels factorials produeixen una sèrie convergent (vegeu nombre e):
• : ${\displaystyle {\frac {1}{1}}+{\frac {1}{1}}+{\frac {1}{2}}+{\frac {1}{6}}+{\frac {1}{24}}+{\frac {1}{120}}+\cdots =e.}$
• Els inversos dels quadrats perfectes produeix una sèrie convergent (vegeu Problema de Basilea):
• : ${\displaystyle {1 \over 1}+{1 \over 4}+{1 \over 9}+{1 \over 16}+{1 \over 25}+{1 \over 36}+\cdots ={\pi ^{2} \over 6}.}$
• Els inversos de les potències de 2 produeix una sèrie convergent:
• : ${\displaystyle {1 \over 1}+{1 \over 2}+{1 \over 4}+{1 \over 8}+{1 \over 16}+{1 \over 32}+\cdots =2.}$
• Els inversos de les potències de qualsevol n són també una sèrie convergent:
• : ${\displaystyle {1 \over 1}+{1 \over n}+{1 \over n^{2}}+{1 \over n^{3}}+{1 \over n^{4}}+{1 \over n^{5}}+\cdots ={n \over n-1}.}$
• Alternar els signes dels inversos de les potències de 2 també produeix una sèrie convergent:
• : ${\displaystyle {1 \over 1}-{1 \over 2}+{1 \over 4}-{1 \over 8}+{1 \over 16}-{1 \over 32}+\cdots ={2 \over 3}.}$
• Alternar el signes dels inversos de les potències de qualsevol n produeix una sèrie convergent:
• : ${\displaystyle {1 \over 1}-{1 \over n}+{1 \over n^{2}}-{1 \over n^{3}}+{1 \over n^{4}}-{1 \over n^{5}}+\cdots ={n \over n+1}.}$
• Els inversos dels nombres de Fibonacci produeix una sèrie convergent (vegeu ψ):
• : ${\displaystyle {\frac {1}{1}}+{\frac {1}{1}}+{\frac {1}{2}}+{\frac {1}{3}}+{\frac {1}{5}}+{\frac {1}{8}}+\cdots =\psi .}$

Tests de convergència

Existeixen diversos mètodes per determinar si una sèrie és convergent o divergent:

Test de comparació directa, Els termes d'una seqüència ${\displaystyle \left\{a_{n}\right\}}$ es comparen amb els d'una altra seqüència ${\displaystyle \left\{b_{n}\right\}}$. Si,

per tot n, ${\displaystyle 0\leq \ a_{n}\leq \ b_{n}}$, i ${\displaystyle \sum _{n=1}^{\infty }b_{n}}$ convergeix, llavors també convergirà ${\displaystyle \sum _{n=1}^{\infty }a_{n}.}$

Tanmateix si:

per tot n, ${\displaystyle 0\leq \ b_{n}\leq \ a_{n}}$, i ${\displaystyle \sum _{n=1}^{\infty }b_{n}}$ divergeix, llavors també ${\displaystyle \sum _{n=1}^{\infty }a_{n}.}$ divergirà.

Criteri de d'Alembert. S'assumeix que per tot n, ${\displaystyle a_{n}>0}$. Suposi's que existeix ${\displaystyle r}$ tal que:

${\displaystyle \lim _{n\to \infty }\left|{\frac {a_{n+1}}{a_{n}}}\right|=r.}$

Si r < 1, llavors la sèrie és convergent. Si r > 1, llavors la sèrie divergeix. Si r = 1, el ratio no és concloent i per tant la sèrie pot convergir o divergir.

Criteri de l'arrel o test de l'n-èsima arrel. S'assumeix també que per tot n, ${\displaystyle a_{n}>0}$. Es defineix ${\displaystyle r}$ com:

${\displaystyle r=\limsup _{n\rightarrow \infty }{\sqrt[{n}]{|a_{n}|}},}$

on "lim sup" denota el límit superior (possiblement ∞; si el límit existeix és el propi valor).

Si r< 1, llavors la sèrie convergeix. Si r > 1, llavors

Com abans, si r < 1, llavors la sèrie és convergent. Si r > 1, llavors la sèrie divergeix. Si r = 1, el ratio no és concloent i per tant la sèrie pot convergir o divergir.

Tant el criteri de d'Alembert com el criteri de l'arrel es basen en la comparació amb sèries geomètriques, i per tant treballen en situacions similars. De fer, si el criteri de d'Alembert funciona (en el sentit que el límit existeix i no és 1) llavors també ho fa el criteri de l'arrel; però la proposició inversa no es compleix. En general, el criteri de l'arrel es pot aplicar més, però en efectes pràctics, el límit és sovint més difícil de calcular en les sèries que es veuen normalment.

Test de l'integral. La sèrie es pot compara a una integral per establir-ne la convergència o divergència. Sigui ${\displaystyle f(n)=a_{n}}$ una funció monòtona descendent. Si:

${\displaystyle \int _{1}^{\infty }f(x)\,dx=\lim _{t\to \infty }\int _{1}^{t}f(x)\,dx<\infty ,}$

llavors la sèrie convergeix. Però si la integral divergeix, llavors la sèrie també.

Test de comparació de límits. Si ${\displaystyle \left\{a_{n}\right\},\left\{b_{n}\right\}>0}$, i el límit ${\displaystyle \lim _{n\to \infty }{\frac {a_{n}}{b_{n}}}}$ existeix i és diferent a 0, totes dues sèries convergeixen o divergeixen.

Criteri de Leibniz. Estableix que per una sèrie alternada de la forma ${\displaystyle \sum _{n=1}^{\infty }a_{n}(-1)^{n}}$, si ${\displaystyle \left\{a_{n}\right\}}$ és monòtonament descendent, i té el límit a 0 en infinit, llavors la sèrie convergeix.

Criteri de condensació de Cauchy. Si ${\displaystyle \left\{a_{n}\right\}}$ és una successió positiva monòtonament descendent, llavors ${\displaystyle \sum _{n=1}^{\infty }a_{n}}$ convergeix si i només si ${\displaystyle \sum _{k=1}^{\infty }2^{k}a_{2^{k}}}$ convergeix.

Test de Dirichlet. El criteri afirma que si ${\displaystyle \{a_{n}\}}$ és una seqüència de nombres reals i ${\displaystyle \{b_{n}\}}$ és una seqüència de nombres complexos i es compleix que:

• ${\displaystyle a_{n+1}\leq a_{n}}$

• ${\displaystyle \lim _{n\rightarrow \infty }a_{n}=0}$

• ${\displaystyle \left|\sum _{n=1}^{N}b_{n}\right|\leq M}$ per tot N enter positiiu

on M és una certa constant, llavors la sèrie

${\displaystyle \sum _{n=1}^{\infty }a_{n}b_{n}}$

convergeix.

Test d'Abel.Suposant que les següents condicions es compleixen:

1. ${\displaystyle \sum a_{n}}$ és una sèrie convergent,
2. ${\displaystyle b_{n}}$ és una successió monòtona i limitada

Llavors ${\displaystyle \sum a_{n}b_{n}}$ és també convergent. Noti's que aquest criteri és especialment peritnent i útil en el cas que ${\displaystyle \sum a_{n}}$ sigui una successió convergent no absoluta (llegeixi's condicional). Pel cas en què sigui absolutament convergent, tot i aplicar-se, és gairebé un corol·lari evident.

Criteri de Raabe. Sigui ${\displaystyle (a_{k})_{k\in \mathbb {N} }}$ una successió tal que ${\displaystyle a_{k}>0}$ ${\displaystyle \forall k\in \mathbb {N} }$. Si existeix el límit

${\displaystyle \lim _{k\rightarrow \infty }k\left(1-{\frac {a_{k+1}}{a_{k}}}\right)=L}$, amb ${\displaystyle L\,\in \,\mathbb {R} }$

aleshores, si ${\displaystyle L>1}$ la sèrie és convergent i si ${\displaystyle L<1}$ la sèrie és divergent.

Convergència condicional i absoluta

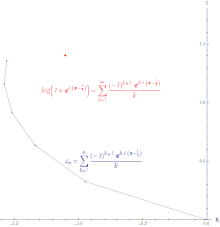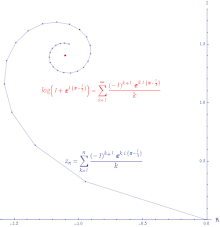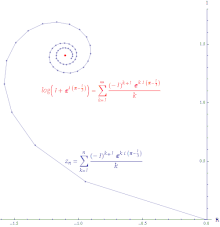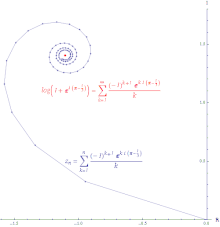
Per a qualsevol seqüència ${\displaystyle \left\{a_{1},\ a_{2},\ a_{3},\dots \right\}}$, ${\displaystyle a_{n}\leq \ \left|a_{n}\right\vert }$ per tot n. Es té que:

${\displaystyle \sum _{n=1}^{\infty }a_{n}\leq \ \sum _{n=1}^{\infty }\left|a_{n}\right\vert .}$

Això significa que si ${\displaystyle \sum _{n=1}^{\infty }\left|a_{n}\right\vert }$ convergeix, llavors ${\displaystyle \sum _{n=1}^{\infty }a_{n}}$ també (però no vice versa). ${\displaystyle \sum _{n=1}^{\infty }a_{n}}$ és, a més, absolutament convergent. Una successió absolutament convergent és aquella en què la longitud de la línia que es crea per unir tots els increments en la suma parcial és finita. La sèrie de potències de la funció exponencial és absolutament convergent a tot arreu.

Si la sèrie ${\displaystyle \sum _{n=1}^{\infty }a_{n}}$ convergeix però la sèrie ${\displaystyle \sum _{n=1}^{\infty }\left|a_{n}\right\vert }$ divergeix, llavors la sèrie ${\displaystyle \sum _{n=1}^{\infty }a_{n}}$ és condicionalment convergent. El camí que es forma en connectar les sumes parcials d'una sèrie condicionalment convergent és inifintament gran. La sèrie de potències del lograitme és condicionalment convergent.

El teorema de sèries de Riemann afirma que si una sèrie convergeix condicionalment, es poden reordenar els termes de la sèrie talment que la sèrie acabi convergint a qualsevol valor, o fins i tot que acabi divergint.

Convergència uniforme

Sigui ${\displaystyle \left\{f_{1},\ f_{2},\ f_{3},\dots \right\}}$ una successió de funcions. La sèries ${\displaystyle \sum _{n=1}^{\infty }f_{n}}$ convergeix uniformement a ${\displaystyle f}$ si la successió ${\displaystyle \{s_{n}\}}$ de sumes parcials definida com:

${\displaystyle s_{n}(x)=\sum _{k=1}^{n}f_{k}(x)}$

convergeix uniformement a ${\displaystyle f}$.

Existeix una analogia del test de comparació per sèries infinites en funcions anomenada prova M de Wierstrass.

Criteri de convergència de Cauchy

El criteri de convergència de Cauchy afirma que una sèrie

${\displaystyle \sum _{n=1}^{\infty }a_{n}}$

convergeix si i només si la successió de sumes parcials és una successió de Cauchy. Això vol dir que per tot ${\displaystyle \varepsilon >0,}$ existeix un enter positiu ${\displaystyle N}$ tal que per tot ${\displaystyle n\geq m\geq N}$ es té:

${\displaystyle \left|\sum _{k=m}^{n}a_{k}\right|<\varepsilon ,}$

que és equivalent a:

${\displaystyle \lim _{n\to \infty \atop m\to \infty }\sum _{k=n}^{n+m}a_{k}=0.}$

Vegeu també

• Convergència (successió matemàtica)

Enllaços externs

• Michiel Hazewinkel (ed.). Series. Encyclopedia of Mathematics (en anglès). Springer, 2001. ISBN 978-1-55608-010-4. 
• Weisstein, Eric (2005). Teorema de les sèries de Riemann. Consultat 16 maig 2005.